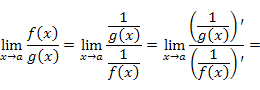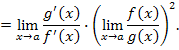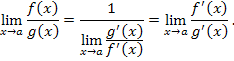| |
Теорема 1.. Пусть функции  и и  определены и дифференцируемы в промежутке определены и дифференцируемы в промежутке 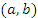 ; ; 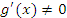 для всех для всех 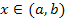 ; ; 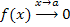 и и 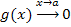 ; существует конечный или бесконечный предел ; существует конечный или бесконечный предел 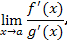 Тогда Тогда
| |
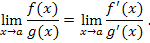
|
(1) |
|
Доказательство. Доопределим функции  и и  в точке x = a, руководствуясь соображениями непрерывности:
Так как в точке x = a, руководствуясь соображениями непрерывности:
Так как 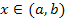 , то по теореме Коши
где , то по теореме Коши
где 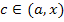 . .
Поскольку существует 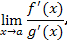 который равен
то существует и предел который равен
то существует и предел 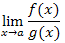 , причем , причем
Теорема 2.. Пусть функции  и и  определены и дифференцируемы в промежутке определены и дифференцируемы в промежутке 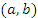 ; ; 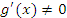 для всех для всех 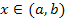 ; ; 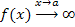 и и  ; существует конечный или бесконечный предел ; существует конечный или бесконечный предел 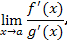 Тогда Тогда
| |
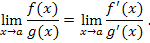
|
(2) |
|
Доказательство. Функции 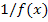 и и 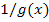 являются бесконечно малыми при являются бесконечно малыми при 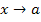 . Тогда по теореме 1
Следовательно, . Тогда по теореме 1
Следовательно,
|
 и
и  определены и дифференцируемы в промежутке
определены и дифференцируемы в промежутке 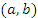 ;
; 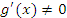 для всех
для всех 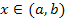 ;
; 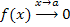 и
и 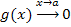 ; существует конечный или бесконечный предел
; существует конечный или бесконечный предел 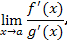 Тогда
Тогда
 и
и  в точке x = a, руководствуясь соображениями непрерывности:
в точке x = a, руководствуясь соображениями непрерывности:
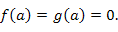
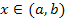 , то по теореме Коши
, то по теореме Коши

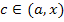 .
.
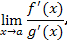 который равен
который равен
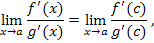
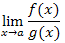 , причем
, причем
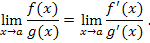
 и
и  определены и дифференцируемы в промежутке
определены и дифференцируемы в промежутке 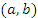 ;
; 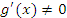 для всех
для всех 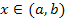 ;
; 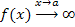 и
и  ; существует конечный или бесконечный предел
; существует конечный или бесконечный предел 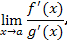 Тогда
Тогда
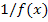 и
и 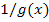 являются бесконечно малыми при
являются бесконечно малыми при 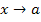 . Тогда по теореме 1
. Тогда по теореме 1