Теорема. Если 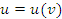 и и 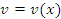 – дифференцируемые функции, то производная сложной функции – дифференцируемые функции, то производная сложной функции 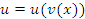 равна равна
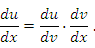
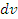 в числителе и знаменателе выражения в правой части этого равенства, то получим тождество. в числителе и знаменателе выражения в правой части этого равенства, то получим тождество.
Формальное доказательство. По определению производной 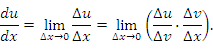
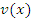 является непрерывной функцией и, следовательно, является непрерывной функцией и, следовательно, 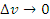 при ∆x → 0. Тогда при ∆x → 0. Тогда
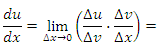
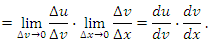
|