Рассмотрим многочлен 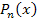 целой степени n: целой степени n:
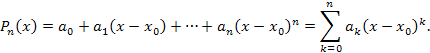
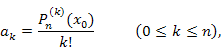
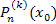 – производные k-го порядка от – производные k-го порядка от 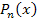 в точке в точке 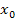 . (Напомним, что . (Напомним, что 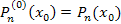 – по определению.) – по определению.)
Очевидно, что  . Найдем производную к-го порядка от многочлена . Найдем производную к-го порядка от многочлена 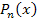 в точке в точке 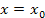 . Заметим, что . Заметим, что
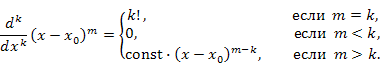
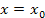 единственной отличной от нуля производной к-го порядка является производная от единственной отличной от нуля производной к-го порядка является производная от 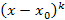 . При этом . При этом  и, таким образом, и, таким образом,
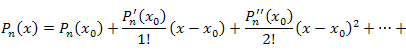
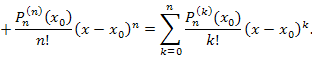
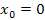 она принимает вид она принимает вид
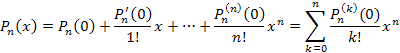
Если оценивать формулу Тейлора для многочленов с позиций ее непосредственного применения для решения практических задач, то результат не покажется особенно впечатляющим. С ее помощью можно, например, преобразовать многочлен целой степени от одного вида к другому. Однако главное значение этой формулы заключается в том, что она устанавливает взаимосвязь между коэффициентами многочлена 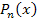 и значениями его производных в точке и значениями его производных в точке 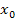 . .
Пример 1. Представить многочлен 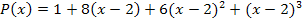
Решение. Согласно формуле Маклорена 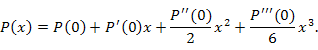
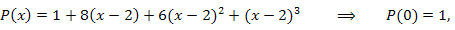
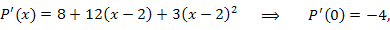

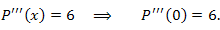
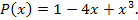


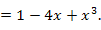
Пример 2. Найти целую часть и остаток от деления многочлена 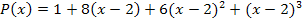 на двучлен на двучлен 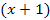 . .
Решение. Представим многочлен 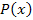 в виде в виде
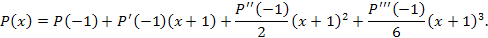

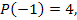 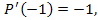  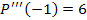 , ,
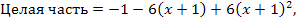

|