Чтобы найти производную функции 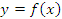 , заданной уравнением в неявном виде, нужно продифференцировать обе части этого уравнения и разрешить полученное уравнение относительно y'. , заданной уравнением в неявном виде, нужно продифференцировать обе части этого уравнения и разрешить полученное уравнение относительно y'.
Пример. Пусть функция 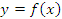 удовлетворяет уравнению удовлетворяет уравнению
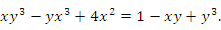

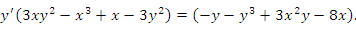
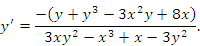
|
Чтобы найти производную функции 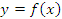 , заданной уравнением в неявном виде, нужно продифференцировать обе части этого уравнения и разрешить полученное уравнение относительно y'. , заданной уравнением в неявном виде, нужно продифференцировать обе части этого уравнения и разрешить полученное уравнение относительно y'.
Пример. Пусть функция 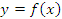 удовлетворяет уравнению удовлетворяет уравнению
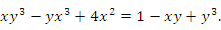

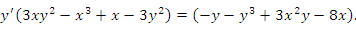
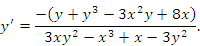
|