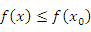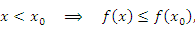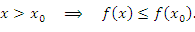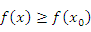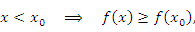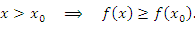Говорят, что функция 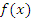 имеет локальный максимум в точке имеет локальный максимум в точке 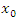 , если , если
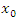 . При этом . При этом 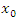 называют точкой локального максимума функции называют точкой локального максимума функции 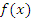 . .
 Неравенство (6) означает, что функция Неравенство (6) означает, что функция 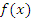 является возрастающей для значений x, расположенных в непосредственной близости к точке локального максимума слева от нее; функция является возрастающей для значений x, расположенных в непосредственной близости к точке локального максимума слева от нее; функция 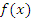 является убывающей для значений x, достаточно близких к этой точке и расположенных справа: является убывающей для значений x, достаточно близких к этой точке и расположенных справа:
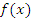 , то , то 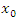 называется точкой абсолютного максимума функции называется точкой абсолютного максимума функции 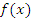 . .
Аналогично, 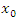 называется точкой локального минимума функции называется точкой локального минимума функции 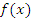 , если , если
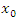 . .
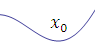 Неравенство (8) означает, что функция Неравенство (8) означает, что функция 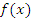 является убывающей для значений x, лежащих слева в непосредственной близости к точке локального минимума и возрастающей – для значений x, расположенных на близком расстоянии справа от этой точки: является убывающей для значений x, лежащих слева в непосредственной близости к точке локального минимума и возрастающей – для значений x, расположенных на близком расстоянии справа от этой точки:
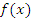 имеет абсолютный максимум в точке имеет абсолютный максимум в точке 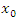 , если неравенство (6) выполняется для всех x из области определения этой функции. , если неравенство (6) выполняется для всех x из области определения этой функции.
Если неравенства в формулах (6) и (8) строгие, то 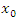 называется точкой строгого локального максимума или минимума соответственно. называется точкой строгого локального максимума или минимума соответственно.
Точками экстремума функции 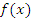 называются точки максимума или минимума этой функции. называются точки максимума или минимума этой функции.
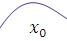
На рисунке 1 представлен фрагмент графика функции 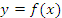 , определенной в промежутке , определенной в промежутке 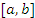 и имеющей локальные экстремумы. и имеющей локальные экстремумы.
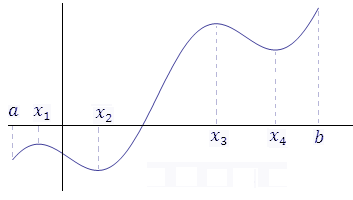
Рис. 1. Точки 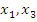 и b являются точками локального максимума. и b являются точками локального максимума.
Точки 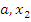 и и 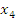 являются точками локального минимума. являются точками локального минимума.
Точка b является точкой абсолютного максимума. Точка 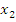 является точкой абсолютного минимума. является точкой абсолютного минимума.
|