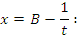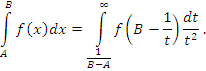Основные понятия
|
В этом разделе речь пойдет об интерпретации символа ∞ в качестые одного из пределов в определенном интеграле. Ничего принципиально нового - обычный предельный переход.
Например, запись вида f(∞) подразумавает число, равное  . |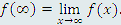
|||||||||
|
К несобственным интегралам относятся:
1) интегралы, у которых хотя бы один из пределов интегрирования равен бесконечности (несобственные интегралы первого рода); 2) интегралы от функций, неограниченных на конечном промежутке интегрирования (несобственные интегралы второго рода). Случай, когда неограниченными являются и сама функция, и промежуток ее интегрирования, не требует отдельного рассмотрения, поскольку он сводится к двум предыдущим случаям разбиением промежутка на части, например, 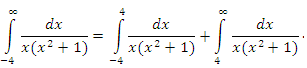 Примеры несобственных интегралов первого рода:
Примеры несобственных интегралов второго рода:
|
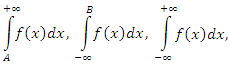
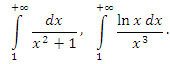
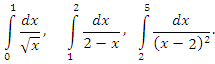
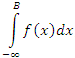с нижним бесконечным пределом может быть преобразован в интеграл 
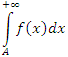с верхним бесконечным пределом подстановкой x = –t; 
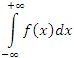с двумя бесконечными пределами может быть преобразован в интегралы с одним бесконечным пределом разбиением промежутка интегрирования на две части и последующей подстановкой x = –t в одном из полученных интегралов;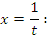 
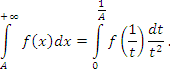
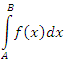второго рода с единственной особой точкой B приводится к несобственному интегралу первого рода подстановкой 
