Под дифференциалом 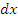 независимого аргумента понимается приращение аргумента: независимого аргумента понимается приращение аргумента:  . Совсем иначе определяется дифференциал функции. Согласно определению предела, равенство . Совсем иначе определяется дифференциал функции. Согласно определению предела, равенство
 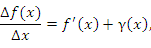 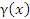 – бесконечно малая функция более высокого порядка по сравнению с ∆x (при ∆x→0). Тогда приращение функции – бесконечно малая функция более высокого порядка по сравнению с ∆x (при ∆x→0). Тогда приращение функции 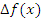 описывается формулой описывается формулой
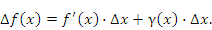 Слагаемое 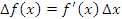 представляет собой линейную (главную) часть приращения функции и называется дифференциалом функции, который обозначается символом представляет собой линейную (главную) часть приращения функции и называется дифференциалом функции, который обозначается символом 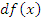 : :
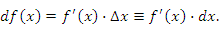
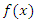 можно представить в виде отношения дифференциалов можно представить в виде отношения дифференциалов 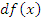 и и 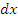 : :
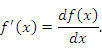
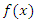 . Теперь же это выражение можно интерпретировать как отношение двух дифференциалов: дифференциала функции к дифференциалу аргумента. . Теперь же это выражение можно интерпретировать как отношение двух дифференциалов: дифференциала функции к дифференциалу аргумента.
|