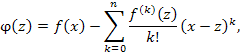Для контроля погрешности вычислений, основанных на использовании формулы Тейлора, полезно располагать различными формами представления остаточного члена, наиболее употребительной из которых является форма Лагранжа,
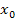 . .
Если 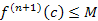 , то , то
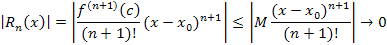
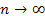 . .
Чем меньше величина 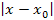 , тем быстрее , тем быстрее 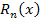 убывает с ростом n. Это означает, что точность аппроксимации функции убывает с ростом n. Это означает, что точность аппроксимации функции  многочленом многочленом
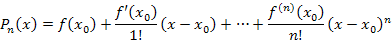
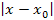 и с увеличением n. и с увеличением n.
Формула Тейлора с остаточным членом в форме Лагранжа имеет следующий вид: 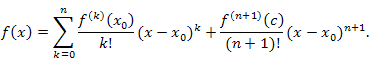
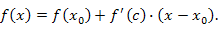
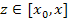 . (Если . (Если 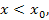 , то полагаем, что , то полагаем, что  ). ).
Отметим, что 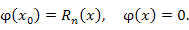
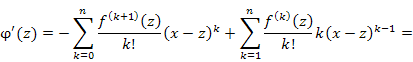

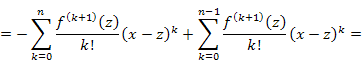
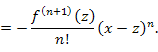
 где где 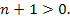 . .
Функции 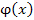 и и 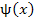 удовлетворяют условиям теоремы Коши и, следовательно, существует такая точка удовлетворяют условиям теоремы Коши и, следовательно, существует такая точка  , что , что
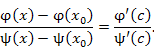

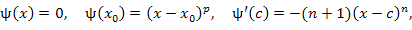
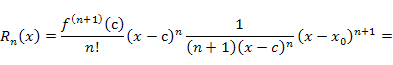
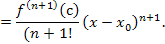
|