Гиперболический синус 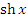 и гиперболический косинус и гиперболический косинус 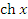 определяются аналитическими выражениями определяются аналитическими выражениями
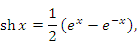

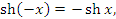
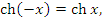
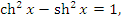
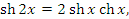

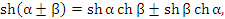

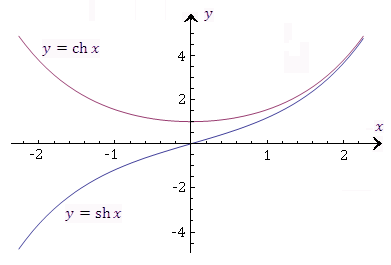
Рис. 3. Графики гиперболических функций 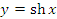 и и  . График гиперболического косинуса называется цепной линией, которая является линией провисания тяжёлой нити, подвешенной в двух точках. . График гиперболического косинуса называется цепной линией, которая является линией провисания тяжёлой нити, подвешенной в двух точках.
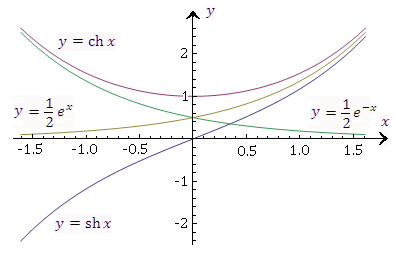
Рис. 4. Сопоставление графиков гиперболических и экспоненциальных функций. Гиперболический тангенс 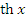 и гиперболический котангенс и гиперболический котангенс 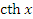 определяются формулами определяются формулами


и представляют собой нечетные функции: 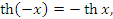

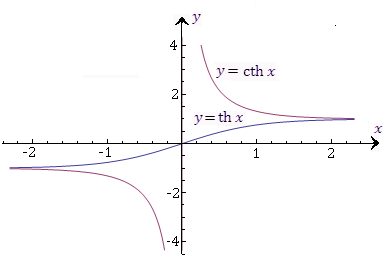
Рис. 5. Графики гиперболических функций 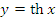 и и  . .

Рис. 6. Сопоставление графиков функций 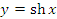 , , 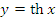 и y = x. и y = x.
|