Дифференциалом второго порядка функции y(x) называется дифференциал первого дифференциала:
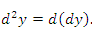
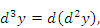
... 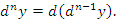
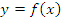 , где x – независимая переменная, то , где x – независимая переменная, то
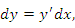
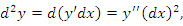
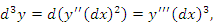
... 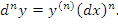
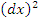 дифференциала независимой переменной x обозначают символом дифференциала независимой переменной x обозначают символом 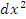 , который читается как "дэ икс дважды"; тогда , который читается как "дэ икс дважды"; тогда 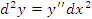 . Аналогично, . Аналогично,
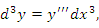
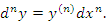
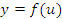 описывает сложную функцию, где u – некоторая функция переменной x. Тогда описывает сложную функцию, где u – некоторая функция переменной x. Тогда
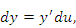
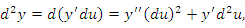
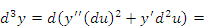
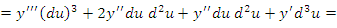
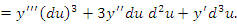
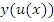 сохраняет свою форму, то есть dy равен произведению производной на дифференциал аргумента. Такое свойство называется инвариантностью формы первого дифференциала. Дифференциалы более высоких порядков свойством инвариантности не обладают. сохраняет свою форму, то есть dy равен произведению производной на дифференциал аргумента. Такое свойство называется инвариантностью формы первого дифференциала. Дифференциалы более высоких порядков свойством инвариантности не обладают.
|