Рассмотрим фрагмент графика функции 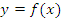 . Выберем на кривой некоторую точку . Выберем на кривой некоторую точку  и придадим аргументу x приращение ∆x. При этом функция y получает приращение ∆y. и придадим аргументу x приращение ∆x. При этом функция y получает приращение ∆y.
Проведем через точки  и и  секущую AB и обозначим символом β угол наклона прямой AB с положительным направлением оси 0x. Касательная к графику функции секущую AB и обозначим символом β угол наклона прямой AB с положительным направлением оси 0x. Касательная к графику функции 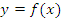 в точке A является предельным положением секущей AB при стремлении приращения ∆x к нулю. Другими словами, если точка B неограниченно приближается к точке A, то в точке A является предельным положением секущей AB при стремлении приращения ∆x к нулю. Другими словами, если точка B неограниченно приближается к точке A, то

Дифференциал 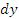 дает линейную часть изменения функции дает линейную часть изменения функции 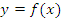 в окрестности точки x, то есть такое приращение, которое получила бы эта функция, если бы она изменялась в окрестности точки x по линейному закону. в окрестности точки x, то есть такое приращение, которое получила бы эта функция, если бы она изменялась в окрестности точки x по линейному закону.
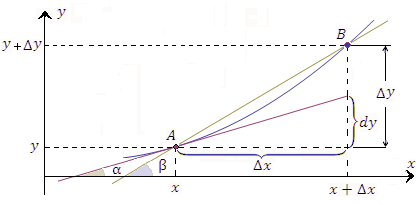
Рис. 7. Дифференциал аргумента есть приращение аргумента. Дифференциал функции “дает прогноз” приращения функции, основанный на характере поведения функции в бесконечно малой окрестности точки. |