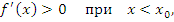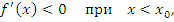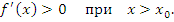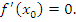Теорема. Пусть функция 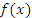 определена в некотором промежутке; имеет локальный экстремум во внутренней точке определена в некотором промежутке; имеет локальный экстремум во внутренней точке 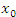 этого промежутка; дифференцируема в окрестности точки этого промежутка; дифференцируема в окрестности точки 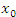 . Если . Если 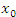 – точка локального максимума, то при переходе через эту точку производная – точка локального максимума, то при переходе через эту точку производная 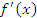 меняет свой знак с плюса на минус: меняет свой знак с плюса на минус:
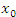 – точка локального минимума, то при переходе через точку – точка локального минимума, то при переходе через точку 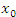 производная производная 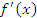 меняет свой знак с минуса на плюс: меняет свой знак с минуса на плюс:
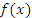 дифференцируема в точке дифференцируема в точке 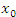 , то , то
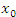 является точкой локального максимума функции является точкой локального максимума функции 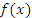 . Тогда эта функция является возрастающей для значений x, расположенных на малых расстояниях слева от точки . Тогда эта функция является возрастающей для значений x, расположенных на малых расстояниях слева от точки 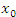 и, следовательно, и, следовательно, 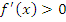 при при 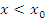 . .
Поскольку функция 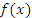 является убывающей для значений x, достаточно близких к точке является убывающей для значений x, достаточно близких к точке 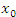 и расположенных справа, то и расположенных справа, то 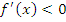 при при 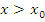 . Таким образом, утверждение (10) доказано. Аналогичным образом устанавливается справедливость утверждения (11). . Таким образом, утверждение (10) доказано. Аналогичным образом устанавливается справедливость утверждения (11).
Теперь предположим, что функция 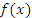 дифференцируема в точке дифференцируема в точке 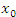 и и 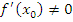 . Поскольку функция . Поскольку функция 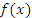 имеет экстремум в точке имеет экстремум в точке 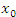 , то справа и слева от точки , то справа и слева от точки 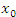 разность разность 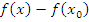 принимает значения противоположных знаков. Если принимает значения противоположных знаков. Если 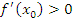 , то функция , то функция 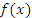 возрастает в окрестности точки возрастает в окрестности точки 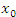 ; если ; если 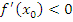 , то функция , то функция 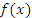 убывает в окрестности точки убывает в окрестности точки 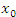 . В обоих случаях . В обоих случаях 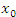 не является точкой экстремума и, таким образом, допущение не является точкой экстремума и, таким образом, допущение 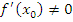 приводит к противоречию с условиями теоремы. приводит к противоречию с условиями теоремы.
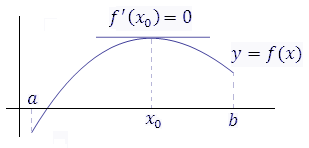
Рис. 1. Касательная к графику функции 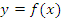 в точке экстремума параллельна оси 0x. в точке экстремума параллельна оси 0x.
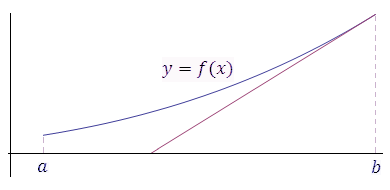
Рис. 2. Если функция принимает свое наибольшее (или наименьшее) значение не во внутренней точке промежутка, а на одном из его концов, то производная этой функции в точке экстремума не обязательно равна нулю. |