-
Опровергнуть теорему Ролля, основываясь на примере функции
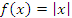 , заданной в промежутке [-2,2]. , заданной в промежутке [-2,2].
Решение. Функция 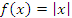 не имеет производной в точке x = 0. Следовательно, условия теоремы Ролля не выполняются. Теорема Ролля устояла. не имеет производной в точке x = 0. Следовательно, условия теоремы Ролля не выполняются. Теорема Ролля устояла.
|
***
***
***
-
Функция
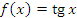 принимает одинаковые значения на концах промежутка принимает одинаковые значения на концах промежутка 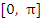 :
Почему для этой функции не выполняется теорема Ролля? :
Почему для этой функции не выполняется теорема Ролля?
-
Показать, что между двумя нулями дифференцируемой функции существует, по крайней мере, один нуль производной этой функции.
|
|