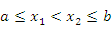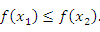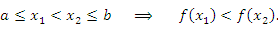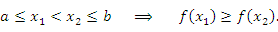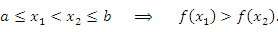Функция 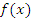 называется монотонной на интервале называется монотонной на интервале 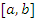 , если ее приращение сохраняет свой знак на этом интервале. , если ее приращение сохраняет свой знак на этом интервале.
Функция 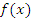 называется неубывающей на интервале называется неубывающей на интервале 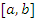 , если условие , если условие
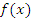 называется возрастающей на интервале называется возрастающей на интервале 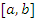 , если , если
Аналогично вводятся понятия невозрастающей функции и убывающей функции. Функция 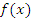 называется невозрастающей на интервале называется невозрастающей на интервале 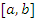 , если , если
Функция 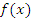 называется убывающей на интервале называется убывающей на интервале 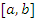 , если , если
Имеется тесная взаимосвязь между поведением функции 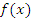 в некотором промежутке и знаком производной в некотором промежутке и знаком производной 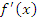 в этом промежутке. Действительно, по определению производной, в этом промежутке. Действительно, по определению производной,
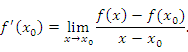
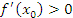 , то существует окрестность точки , то существует окрестность точки 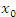 , в которой разностное отношение под знаком предела остается положительным: , в которой разностное отношение под знаком предела остается положительным:
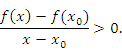

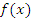 является возрастающей в окрестности точки является возрастающей в окрестности точки 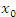 . .
Предположим теперь, что функция 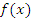 является неубывающей в окрестности точки является неубывающей в окрестности точки 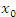 . Тогда . Тогда
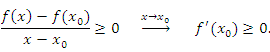
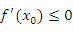
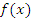 была невозрастающей в окрестности точки была невозрастающей в окрестности точки 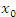 . .
|