Теорема. Если функция 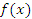 дифференцируема в некоторой точке a, то она непрерывна в этой точке. дифференцируема в некоторой точке a, то она непрерывна в этой точке.
Доказательство. По определению производной 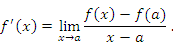
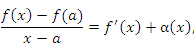
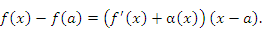
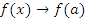 при x → a. при x → a.
Заметим, что дифференцируемость функции в некоторой точке означает ее гладкость в окрестности этой точки, что влечет за собой непрерывность функции в рассматриваемой точке. Однако обратное утверждение несправедливо – функция, обладающая свойством непрерывности в некоторой точке, не обязательно дифференцируема в этой точке. 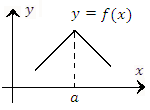
Рис. 8. Непрерывная в точке a функция 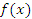 не является дифференцируемой в этой точке. не является дифференцируемой в этой точке.
|