Формулу Тейлора
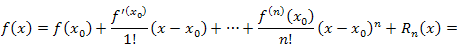
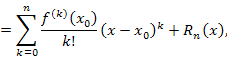
Разность  есть приращение аргумента, то есть дифференциал аргумента: есть приращение аргумента, то есть дифференциал аргумента:


 представляет собой соответствующее приращение функции: представляет собой соответствующее приращение функции:

 в точке в точке 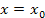 равен равен

 k-го порядка в точке равен k-го порядка в точке равен


|
Формулу Тейлора
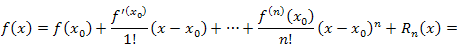
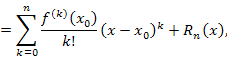
Разность  есть приращение аргумента, то есть дифференциал аргумента: есть приращение аргумента, то есть дифференциал аргумента:


 представляет собой соответствующее приращение функции: представляет собой соответствующее приращение функции:

 в точке в точке 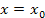 равен равен

 k-го порядка в точке равен k-го порядка в точке равен


|