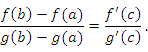Теорема. Пусть функции 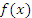 и и 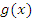 непрерывны в замкнутом промежутке непрерывны в замкнутом промежутке 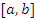 ; дифференцируемы в открытом промежутке ; дифференцируемы в открытом промежутке 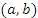 ; ; 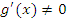 в открытом промежутке в открытом промежутке 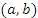 . Тогда существует такая точка . Тогда существует такая точка 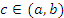 , что , что
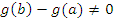 . В противном случае – согласно теореме Ролля – производная . В противном случае – согласно теореме Ролля – производная 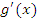 обратилась бы в нуль в некоторой точке обратилась бы в нуль в некоторой точке 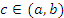 . .
Рассмотрим вспомогательную функцию 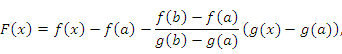
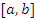 : :
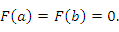
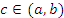 , в которой , в которой
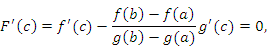
Следствие. Теорема Лагранжа является частным случаем теоремы Коши при 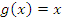 . В свою очередь теорема Ролля представляет собой частный случай теоремы Лагранжа. Таким образом, теорема Коши включает в себя в качестве частных случаев теорему Ролля и теорему Лагранжа. . В свою очередь теорема Ролля представляет собой частный случай теоремы Лагранжа. Таким образом, теорема Коши включает в себя в качестве частных случаев теорему Ролля и теорему Лагранжа.
|