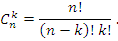| |
Предположим, что функции  и и  дифференцируемы вместе со своими производными до n-го порядка включительно. Применяя правило дифференцирования произведения двух функций, получим
Сопоставим эти выражения со степенями бинома дифференцируемы вместе со своими производными до n-го порядка включительно. Применяя правило дифференцирования произведения двух функций, получим
Сопоставим эти выражения со степенями бинома 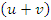 :
Бросается в глаза правило соответствия: чтобы получить формулу для производной 1-го, 2-го или 3-го порядков от произведения функций :
Бросается в глаза правило соответствия: чтобы получить формулу для производной 1-го, 2-го или 3-го порядков от произведения функций  и и  , нужно заменить степени , нужно заменить степени 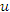 и и 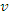 в выражении для в выражении для 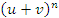 (где n = 1,2,3) производными соответствующих порядков. Кроме того, нулевые степени величин (где n = 1,2,3) производными соответствующих порядков. Кроме того, нулевые степени величин 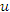 и и 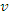 следует заменить производными нулевого порядка, подразумевая под ними функции следует заменить производными нулевого порядка, подразумевая под ними функции  и и  : :
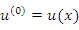  .
Обобщая это правило на случай производной произвольного порядка n, получим формулу Лейбница,
где 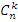 - биномиальные коэффициенты:
Строгое доказательство формулы Лейбница основывается на методе математической индукции. - биномиальные коэффициенты:
Строгое доказательство формулы Лейбница основывается на методе математической индукции.
|
 и
и  дифференцируемы вместе со своими производными до n-го порядка включительно. Применяя правило дифференцирования произведения двух функций, получим
дифференцируемы вместе со своими производными до n-го порядка включительно. Применяя правило дифференцирования произведения двух функций, получим
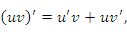
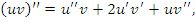

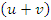 :
:

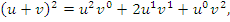
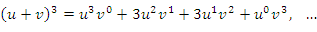
 и
и  , нужно заменить степени
, нужно заменить степени 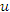 и
и 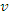 в выражении для
в выражении для 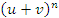 (где n = 1,2,3) производными соответствующих порядков. Кроме того, нулевые степени величин
(где n = 1,2,3) производными соответствующих порядков. Кроме того, нулевые степени величин 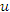 и
и 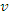 следует заменить производными нулевого порядка, подразумевая под ними функции
следует заменить производными нулевого порядка, подразумевая под ними функции  и
и  :
:
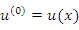
 .
.
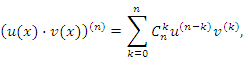
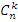 - биномиальные коэффициенты:
- биномиальные коэффициенты: