Теорема 2. Остаточный член 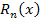 разложения функции по формуле Тейлора является бесконечно малой более высокого порядка по сравнению с разложения функции по формуле Тейлора является бесконечно малой более высокого порядка по сравнению с 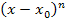 при при 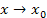 : :
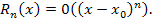
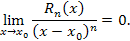
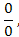 для раскрытия которой можно использовать правило Лопиталя: для раскрытия которой можно использовать правило Лопиталя:
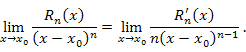
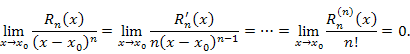
|
Теорема 2. Остаточный член 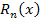 разложения функции по формуле Тейлора является бесконечно малой более высокого порядка по сравнению с разложения функции по формуле Тейлора является бесконечно малой более высокого порядка по сравнению с 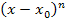 при при 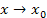 : :
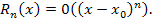
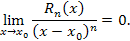
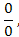 для раскрытия которой можно использовать правило Лопиталя: для раскрытия которой можно использовать правило Лопиталя:
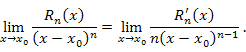
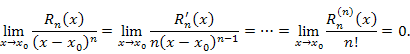
|