Математическое понятие числовой последовательности находится в полном соответствии с нашим интуитивным представлением о последовательности событий, что подразумевает их конкретный порядок. Говоря о числовой последовательности, мы имеем в виду множество значений функции натурального аргумента. Для обозначения последовательностей используются выражения вида 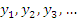 или или 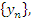 где где 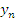 – общий член последовательности, определяющий все ее элементы. – общий член последовательности, определяющий все ее элементы.
Последовательность 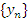 называется монотонно возрастающей, если каждый ее последующий член больше предыдущего: называется монотонно возрастающей, если каждый ее последующий член больше предыдущего: 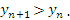
Последовательность 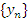 называется монотонно убывающей, если каждый ее последующий член меньше предыдущего: называется монотонно убывающей, если каждый ее последующий член меньше предыдущего: 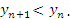
Элементам числовой последовательности можно поставить в соответствие точки числовой оси: 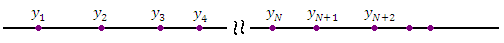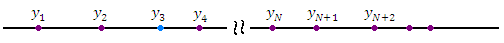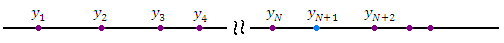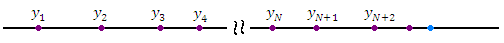
Существуют и другие способы графического представления элементов последовательности, например, в виде графика функции 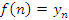 : :
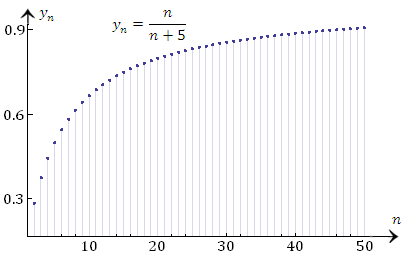
Рис. 1. Графическая иллюстрация монотонно возрастающей последовательности. 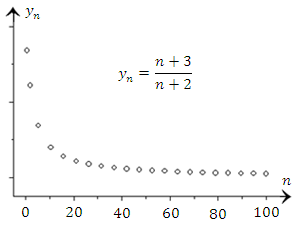
Рис. 2. Монотонно убывающая последовательность. |