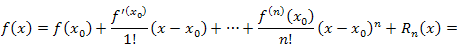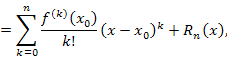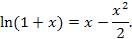Теорема 1. Если функция 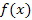 имеет в точке имеет в точке 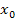 производные до n-го порядка включительно, то ее можно представить в виде производные до n-го порядка включительно, то ее можно представить в виде
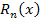 (остаточный член разложения) и ее производные до n-го порядка включительно обращаются в нуль в точке (остаточный член разложения) и ее производные до n-го порядка включительно обращаются в нуль в точке 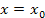 : :
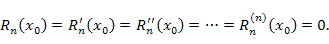 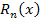 при при 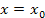 вытекает непосредственно из уравнения (1): вытекает непосредственно из уравнения (1):
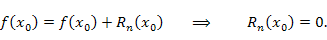 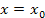 . Заметим, что . Заметим, что
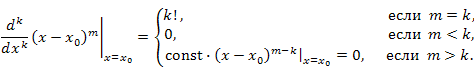 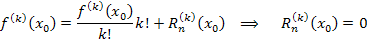 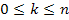 , что и требовалось доказать. , что и требовалось доказать.
Формула (1) называется формулой Тейлора с остаточным членом 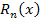 , а ее частный случай при , а ее частный случай при 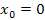 – формулой Маклорена: – формулой Маклорена:
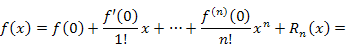
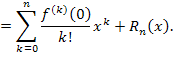
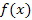 в точке в точке 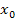 влечет за собой ее непрерывность в некоторой окрестности этой точки, а обращение в нуль в точке влечет за собой ее непрерывность в некоторой окрестности этой точки, а обращение в нуль в точке 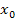 остаточного члена остаточного члена 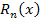 и его производной (то есть быстроты изменения в окрестности точки и его производной (то есть быстроты изменения в окрестности точки 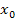 ) означает, что ) означает, что 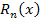 принимает малые значения – по крайней мере - в непосредственной близости от точки принимает малые значения – по крайней мере - в непосредственной близости от точки 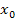 . Следовательно, формула Тейлора может использоваться для аппроксимации функций многочленами. При этом остаточный член . Следовательно, формула Тейлора может использоваться для аппроксимации функций многочленами. При этом остаточный член 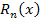 рассматривается как погрешность аппроксимации и отбрасывается: рассматривается как погрешность аппроксимации и отбрасывается:
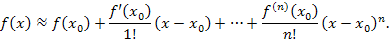
Пример 3. Найти линейную аппроксимацию функции 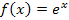 в окрестности нулевой точки. в окрестности нулевой точки.
Решение. Учитывая, что 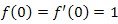 , и подставляя в формулу (1) эти значения, получаем , и подставляя в формулу (1) эти значения, получаем
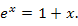
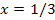 отличие приближенного значения от точного результата составляет менее 4.5%. С уменьшением абсолютной величины x точность вычислений существенно возрастает. Так, при отличие приближенного значения от точного результата составляет менее 4.5%. С уменьшением абсолютной величины x точность вычислений существенно возрастает. Так, при 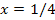 ошибка вычисления становится примерно равной 2.65%. ошибка вычисления становится примерно равной 2.65%.
Вычитая из обеих частей последнего равенства единицу и переходя к пределу 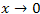 , получаем соотношение , получаем соотношение
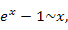
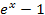 и x при и x при 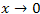 . .
Пример 4. Найти квадратичную аппроксимацию функции 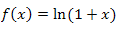 в окрестности нулевой точки. в окрестности нулевой точки.
Решение. Очевидно, что 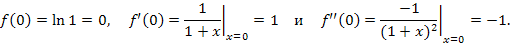
 при малых (по абсолютной величине) значениях x – по сравнению с соотношением при малых (по абсолютной величине) значениях x – по сравнению с соотношением
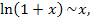
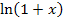 и x при и x при 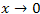 . .
Отметим, в частности, что формула (2) при 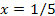 дает для дает для 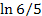 число 0.18, тогда как точным значением является 0.18232… число 0.18, тогда как точным значением является 0.18232…
|