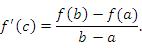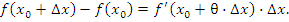Теорема. Пусть функция  дифференцируема в открытом промежутке дифференцируема в открытом промежутке  и сохраняет непрерывность на концах этого промежутка. Тогда существует такая точка и сохраняет непрерывность на концах этого промежутка. Тогда существует такая точка 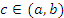 , что , что
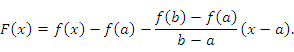
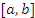 , а на его концах принимает одинаковые значения: , а на его концах принимает одинаковые значения:
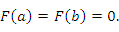
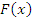 удовлетворяет всем условиям теоремы Ролля и, следовательно, существует точка удовлетворяет всем условиям теоремы Ролля и, следовательно, существует точка 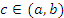 , в которой производная функции , в которой производная функции 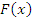 равна нулю: равна нулю:
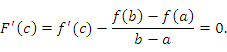
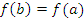 , из теоремы Лагранжа вытекает, что существует точка , из теоремы Лагранжа вытекает, что существует точка 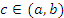 , в которой производная функции , в которой производная функции 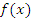 равна нулю: равна нулю: 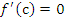 . Это означает, что теорема Лагранжа является обобщением теоремы Ролля. . Это означает, что теорема Лагранжа является обобщением теоремы Ролля.
Следствие 2. Если 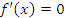 во всех точках некоторого промежутка во всех точках некоторого промежутка 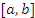 , то , то 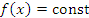 в этом промежутке. в этом промежутке.
Действительно, пусть 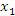 и и 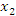 – произвольные точки промежутка – произвольные точки промежутка 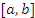 и и 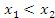 . Применяя теорему Лагранжа к промежутку . Применяя теорему Лагранжа к промежутку 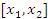 , получим , получим
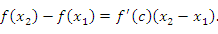
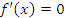 во всех точках промежутка во всех точках промежутка 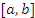 . Тогда . Тогда
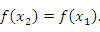
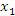 и и 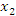 , получаем требуемое утверждение. , получаем требуемое утверждение.
Геометрическая интерпретация теоремы Лагранжа. Разностное отношение в правой части формулы (13) есть угловой коэффициент секущей, проходящей через точки 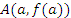 и и 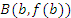 , а производная , а производная 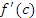 равна угловому коэффициенту касательной к графику функции равна угловому коэффициенту касательной к графику функции 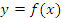 в некоторой средней точке промежутка в некоторой средней точке промежутка 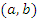 . Поэтому за теоремой Лагранжа закрепилось название “теорема о среднем”. . Поэтому за теоремой Лагранжа закрепилось название “теорема о среднем”.
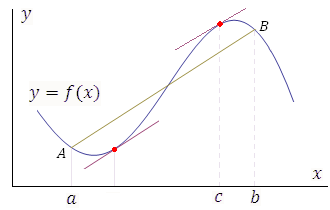
Рис. 6. Теорема Лагранжа устанавливает условия существования хотя бы одной точки c, в которой касательная к графику функции 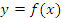 параллельна секущей AB. Таких точек может быть несколько. параллельна секущей AB. Таких точек может быть несколько.
Физическая интерпретацию теоремы Лагранжа. Пусть функция 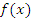 описывает смещение частицы из начального положения в зависимости от времени x ее движения по прямой. Тогда разностное отношение описывает смещение частицы из начального положения в зависимости от времени x ее движения по прямой. Тогда разностное отношение
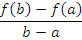
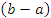 , а производная , а производная 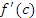 – мгновенную скорость движения частицы в момент времени c. Существует такой момент времени, в который мгновенная скорость движения равна средней скорости. – мгновенную скорость движения частицы в момент времени c. Существует такой момент времени, в который мгновенная скорость движения равна средней скорости.
Отметим, что формула (13) сохраняет свою справедливость и при b < a. Если применить теорему Лагранжа к промежутку 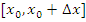 и представить значение c в виде и представить значение c в виде
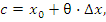
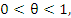 то формула (13) примет вид то формула (13) примет вид
|