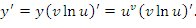Рассмотрим проблему дифференцирования функций вида 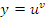 , где , где 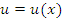 и и 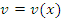 – некоторые дифференцируемые функции. Используя логарифмические тождества – некоторые дифференцируемые функции. Используя логарифмические тождества
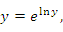
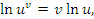
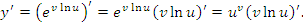
Таким образом, проблема нахождения производных от функций вида 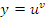 сводится к процедуре дифференцирования произведения функций. К такому же результату приводит логарифмическое дифференцирование функции сводится к процедуре дифференцирования произведения функций. К такому же результату приводит логарифмическое дифференцирование функции 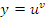 , под которым понимается предварительное логарифмирование функции и последующее дифференцирование полученного выражения: , под которым понимается предварительное логарифмирование функции и последующее дифференцирование полученного выражения:
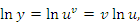
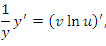
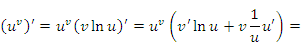
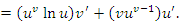
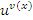 , где основание u формально рассматривается как константа. Второе слагаемое можно интерпретировать как результат дифференцирования степенной функции , где основание u формально рассматривается как константа. Второе слагаемое можно интерпретировать как результат дифференцирования степенной функции 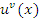 , если формально считать, что , если формально считать, что 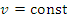 . .
Логарифмическое дифференцирование существенно упрощает процедуру вычисления производных от выражений вида 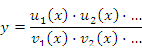
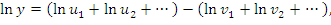
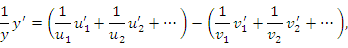
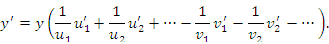
|