Пусть 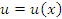 и и 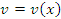 – дифференцируемые функции; c – постоянный множитель. Тогда – дифференцируемые функции; c – постоянный множитель. Тогда
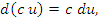

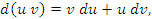
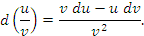
Доказательство. Чтобы проверить справедливость этих равенств, достаточно разделить их правые и левые части на dx. Тогда мы получим стандартные формулы дифференцирования суммы, произведения и частного от деления функций: 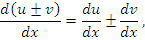
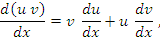
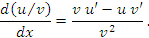
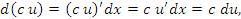
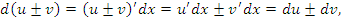
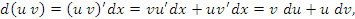
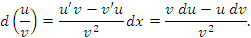
|