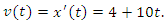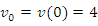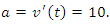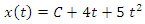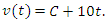|
Пусть над переменной x выполнена некоторая математическая операция, например, операция возведения в третью стеень. Для возврата к исходному состоянию достаточно выполнить обратное преобразование – применить к полученному результату операцию извлечения корня третьей степени:

Порядок операций можно изменить: сначала извлечь корень третьей степени, а затем возвести полученный результат в третью стеень: 
Этот пример иллюстрирует принципиально важное обстоятельство: сопоставление каждой математической операции обратного преобразования, что позволяет решать обратную задачу. Дифференцирование и интегрирование функции являются взаимно обратными операциями. Одна из этих операций "отменяет" другую. |
|||||||||||||||||||||||||
Пусть при движении частицы вдоль оси 0x зависимость x-координаты от времени t описывается уравнением
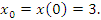
Скорость движения частицы равна производной от координаты по времени и, следовательно,
Рассмотрим теперь обратную задачу, когда по заданной зависимости скорости движения частицы от времени нужно определить положение частицы в произвольный момент времени. Заметим, что уравнение (2) не содержит информации о положении частицы в начальный момент времени. Такие сведения оказались утерянными в результате дифференцирования уравнения движения (1). Следовательно, для однозначного решения обратной задачи, а именно – восстановления функции  по известной ее производной по известной ее производной 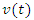 – необходимо дополнительно задать начальное условие – необходимо дополнительно задать начальное условие 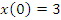 . В противном случае общее решение такой задачи должно содержать неопределенную постоянную величину: . В противном случае общее решение такой задачи должно содержать неопределенную постоянную величину:
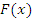 по заданной производной по заданной производной 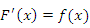 этой функции называется интегрированием функции этой функции называется интегрированием функции 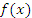 . .
Функция общего вида 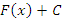 , полученная в результате интегрирования, называется неопределенным интегралом, а любое частное решение , полученная в результате интегрирования, называется неопределенным интегралом, а любое частное решение 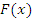 такого рода задачи – первообразной исходной функции. такого рода задачи – первообразной исходной функции.
В этих терминах задача нахождения функции  по известной ее производной по известной ее производной 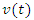 является стандартной проблемой интегрирования функции является стандартной проблемой интегрирования функции 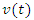 . При этом решение вида (5) представляет собой неопределенный интеграл от функции . При этом решение вида (5) представляет собой неопределенный интеграл от функции 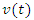 , тогда как решение вида (1) есть первообразная функции , тогда как решение вида (1) есть первообразная функции 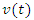 . .
|
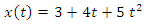 ,
,