Пусть n – произвольное вещественное число. Тогда
 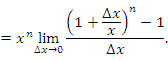
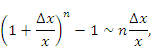  Пусть 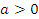 и и 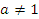 . Тогда . Тогда

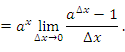 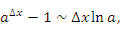 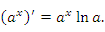 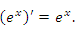
 является уникальной, ибо это единственная функция, производная от которой совпадает с самой функцией. является уникальной, ибо это единственная функция, производная от которой совпадает с самой функцией.
Покажем, что для любого x > 0 выполняется следующее правило дифференцирования логарифмической функции: 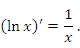
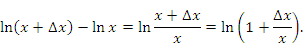
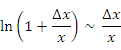
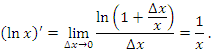
|