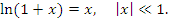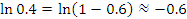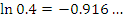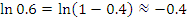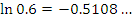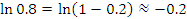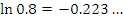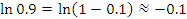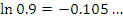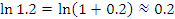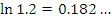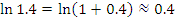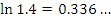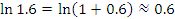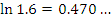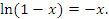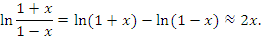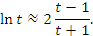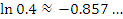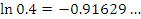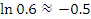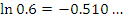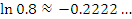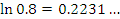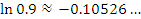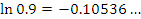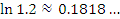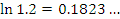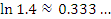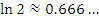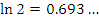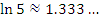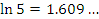| |
Теорема 3 устанавливает, что в некоторой достаточно малой окрестности нуля справедливо следующее приближенное равенство:
| |
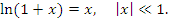
|
(1) |
|
Эта формула пригодна для оценки натуральных логарифмов, аргументы которых близки к 1. Сравним результаты приближенных вычислений логарифмов с соответствующими точными значениями.
Как и следовало ожидать, погрешность вычислений 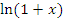 заметно возрастает с ростом заметно возрастает с ростом 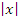 .
Чтобы повысить точность вычислений и получить другую аппроксимирующую формулу, позволяющую расширить диапазон допустимых значений x, запишем равенство (1) в виде .
Чтобы повысить точность вычислений и получить другую аппроксимирующую формулу, позволяющую расширить диапазон допустимых значений x, запишем равенство (1) в виде
| |
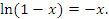
|
(2) |
|
Тогда
| |
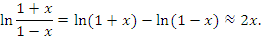 |
(3) |
|
Если, например, 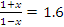 , то , то 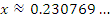 , а результатом вычислений по формуле (2) является число
которое отличается от точного значения менее чем на 0.01. , а результатом вычислений по формуле (2) является число
которое отличается от точного значения менее чем на 0.01.
Очевидно, что решение уравнения
имеет вид
Тогда
| |
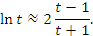
|
(4) |
|
Результаты вычислений логарифмов по этой формуле представлены в таблице.
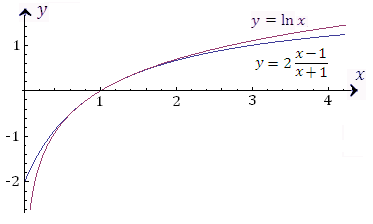 Рис. 16
Рис. 16. Графики функций 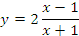 и y = ln x.
|
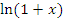 заметно возрастает с ростом
заметно возрастает с ростом 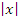 .
Чтобы повысить точность вычислений и получить другую аппроксимирующую формулу, позволяющую расширить диапазон допустимых значений x, запишем равенство (1) в виде
.
Чтобы повысить точность вычислений и получить другую аппроксимирующую формулу, позволяющую расширить диапазон допустимых значений x, запишем равенство (1) в виде
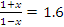 , то
, то 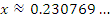 , а результатом вычислений по формуле (2) является число
, а результатом вычислений по формуле (2) является число
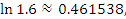
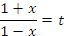
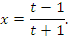
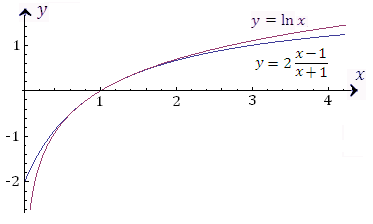
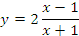 и y = ln x.
и y = ln x.