Свойство 1. Произведение бесконечно малой последовательности 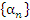 и ограниченной последовательности и ограниченной последовательности 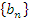 есть бесконечно малая последовательность есть бесконечно малая последовательность 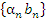 . .
Доказательство. Ограниченность последовательности 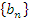 означает, что означает, что 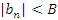 для всех для всех 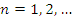 , где B – некоторое положительное число. Выберем сколь угодно малое число ε > 0. Согласно определению бесконечно малой последовательности существует такой номер N, начиная с которого величины , где B – некоторое положительное число. Выберем сколь угодно малое число ε > 0. Согласно определению бесконечно малой последовательности существует такой номер N, начиная с которого величины 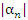 становятся меньше любого положительного числа и, в частности, становятся меньше любого положительного числа и, в частности, 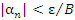 . Тогда . Тогда
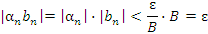
Следствие. Умножиение бесконечно малой последовательности на любое число дает бесконечно малую последовательность. Свойство 2. Сумма любого конечного числа бесконечно малых величин есть величина бесконечно малая. Доказательство. Рассмотрим сначала сумму двух бесконечно малых величин 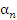 и и 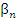 . .
Пусть ε – произвольное положительное число. Тогда существуют номер 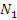 , начиная с которого бесконечно малые величины , начиная с которого бесконечно малые величины 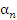 становятся меньше числа становятся меньше числа 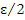 : :
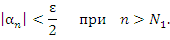
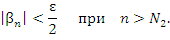
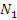 и и 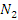 . Тогда для всех номеров n > N выполняется неравенство . Тогда для всех номеров n > N выполняется неравенство
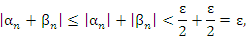
Переходя к случаю суммы произвольного конечного числа бесконечно малых величин, заметим, что любая пара бесконечно малых в этой сумме может быть представлена одной бесконечно малой. Затем каждая пара полученных бесконечно малых может быть заменена одной бесконечно малой и так далее, что в конечном итоге позволит свести рассматриваемую сумму к единственной бесконечно малой. |