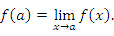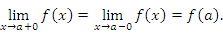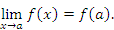| |
Функция 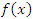 называется непрерывной в точке a, если она определена в этой точке и называется непрерывной в точке a, если она определена в этой точке и
| |
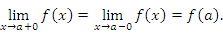
|
(1) |
|
Условие непрерывности (1) можно также записать в виде
| |
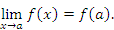
|
(2) |
|
Функция 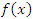 непрерывна на множестве, если она непрерывна в каждой точке этого множества. Если же непрерывность функции нарушается в некоторой точке, то такая точка называется точкой разрыва. Точки разрыва можно классифицировать по величине модуля разности между односторонними пределами, непрерывна на множестве, если она непрерывна в каждой точке этого множества. Если же непрерывность функции нарушается в некоторой точке, то такая точка называется точкой разрыва. Точки разрыва можно классифицировать по величине модуля разности между односторонними пределами,
который называют скачком функции при переходе через точку a. Если этот скачок равен нулю, но функция 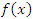 не определена в точке a, то такая точка называется точкой устранимого разрыва. Например, функция не определена в точке a, то такая точка называется точкой устранимого разрыва. Например, функция 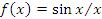 не определена в нуле, однако ее предел в этой точке существует и равен 1. Поэтому для устранения разрыва достаточно доопределить функцию не определена в нуле, однако ее предел в этой точке существует и равен 1. Поэтому для устранения разрыва достаточно доопределить функцию 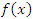 при x = 0, исходя из соображений непрерывности:
В случае произвольной функции при x = 0, исходя из соображений непрерывности:
В случае произвольной функции 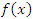 , для которой точка a является точкой устранимого разрыва, нужно расширить область определения функции, включив в нее точку a и полагая
Если скачок функции в точке a имеет конечное значение, то эту точку называют точкой разрыва первого рода. Скачок функции в точке a равен бесконечности, если какой-либо односторонний предел равен бесконечности. В этом случае говорят о точке разрыва второго рода. , для которой точка a является точкой устранимого разрыва, нужно расширить область определения функции, включив в нее точку a и полагая
Если скачок функции в точке a имеет конечное значение, то эту точку называют точкой разрыва первого рода. Скачок функции в точке a равен бесконечности, если какой-либо односторонний предел равен бесконечности. В этом случае говорят о точке разрыва второго рода.
|
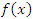 называется непрерывной в точке a, если она определена в этой точке и
называется непрерывной в точке a, если она определена в этой точке и
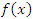 непрерывна на множестве, если она непрерывна в каждой точке этого множества. Если же непрерывность функции нарушается в некоторой точке, то такая точка называется точкой разрыва. Точки разрыва можно классифицировать по величине модуля разности между односторонними пределами,
непрерывна на множестве, если она непрерывна в каждой точке этого множества. Если же непрерывность функции нарушается в некоторой точке, то такая точка называется точкой разрыва. Точки разрыва можно классифицировать по величине модуля разности между односторонними пределами,
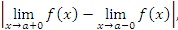
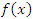 не определена в точке a, то такая точка называется точкой устранимого разрыва. Например, функция
не определена в точке a, то такая точка называется точкой устранимого разрыва. Например, функция 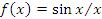 не определена в нуле, однако ее предел в этой точке существует и равен 1. Поэтому для устранения разрыва достаточно доопределить функцию
не определена в нуле, однако ее предел в этой точке существует и равен 1. Поэтому для устранения разрыва достаточно доопределить функцию 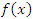 при x = 0, исходя из соображений непрерывности:
при x = 0, исходя из соображений непрерывности:
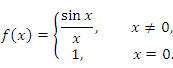
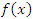 , для которой точка a является точкой устранимого разрыва, нужно расширить область определения функции, включив в нее точку a и полагая
, для которой точка a является точкой устранимого разрыва, нужно расширить область определения функции, включив в нее точку a и полагая