|
Теорема 3. Всякая ограниченная сверху монотонно возрастающая последовательность имеет конечный предел.
Доказательство. Пусть A – наименьшая верхняя граница последовательности 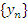 . Это означает, что . Это означает, что
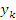 , превосходящий число A – ε: , превосходящий число A – ε:
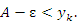
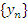 является монотонно возрастающей, то является монотонно возрастающей, то
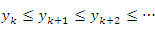
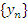 , начиная с , начиная с 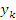 , удовлетворяют неравенству , удовлетворяют неравенству
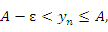
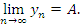
Теорема 4. Всякая ограниченная снизу монотонно убывающая последовательность имеет конечный предел. Доказательство этой теоремы по своей сути не отличается от доказательства предыдущей теоремы и предоставляется читателю. |
 ;
;