Последовательность 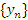 называется бесконечно большой (б/б), если абсолютные величины всех ее элементов – начиная с некоторого номера N – превышают любое сколь угодно большое наперед заданное число E > 0. Другими словами, называется бесконечно большой (б/б), если абсолютные величины всех ее элементов – начиная с некоторого номера N – превышают любое сколь угодно большое наперед заданное число E > 0. Другими словами, 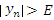 при n > N. при n > N.
Легко показать, что общий член 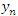 бесконечно большой последовательности может быть представлен в виде бесконечно большой последовательности может быть представлен в виде
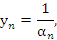
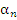 –некоторая бесконечно малая последовательность. –некоторая бесконечно малая последовательность.
Чтобы наглядно представить себе смысл термина “бесконечно большая величина”, поделите число 1 на 0.1, затем на 0.01, 0.001, 0.000001 и так далее. Понятие бесконечно большой последовательности можно также сформулировать в терминах E-окрестности бесконечно удаленной точки. Говорят, что элементы содержатся в E-окрестности бесконечно удаленной точки, если их абсолютные величины превосходят число E. Другими словами, под E-окрестностью бесконечно удаленной точки понимается один из интервалов 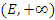 или или 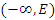 , либо оба эти интервалы. Можно также сказать, что последовательность является бесконечно большой, если все ее элементы, начиная с некоторого номера, попадают в E-окрестность бесконечно удаленной точки. , либо оба эти интервалы. Можно также сказать, что последовательность является бесконечно большой, если все ее элементы, начиная с некоторого номера, попадают в E-окрестность бесконечно удаленной точки.
Для обозначения бесконечно больших последовательностей используются символические выражения вида 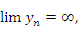
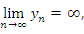
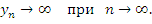
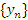 имеет бесконечный предел или что переменная имеет бесконечный предел или что переменная 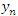 стремится к бесконечности. стремится к бесконечности.
Очевидно, что любая бесконечно большая последовательность является неограниченной и расходящейся. Типичные особенности поведения бесконечно больших величин при 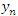 показаны на рисунке 14. показаны на рисунке 14.
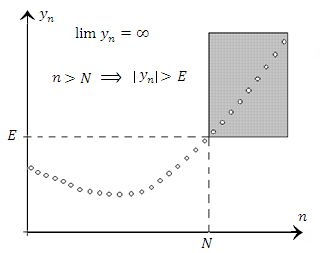
Рис. 14. Пример расходящейся последовательности 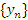 . .
Утверждение, что последовательность 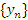 является бесконечно большой, а ее элементы сохраняют знак “+” (по крайней мере для достаточно больших номеров), записывается в виде является бесконечно большой, а ее элементы сохраняют знак “+” (по крайней мере для достаточно больших номеров), записывается в виде 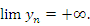 и иллюстрируется рисунком 15. и иллюстрируется рисунком 15.
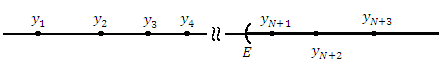
Рис. 15. Последовательность 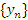 , элементы которой стремятся к + ∞ при , элементы которой стремятся к + ∞ при 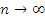 . .
Аналогичным образом интерпретируется выражение вида 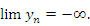 . .
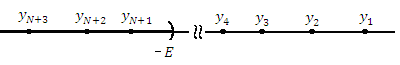
Рис. 16. Бесконечно большая последовательность, элементы которой сохраняют знак “–” для достаточно больших номеров n. |