Теорема. Последовательность с общим членом 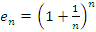 имеет конечный предел при имеет конечный предел при 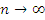 . .
Замечание. Для обозначения этого предела используется символ e: 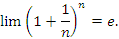
e = 2.71828182845904523536028747135266249775724709… Доказательство. Покажем сначала, что 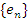 представляет собой монотонно возрастающую последовательность. Согласно биному Ньютона, представляет собой монотонно возрастающую последовательность. Согласно биному Ньютона,
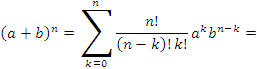
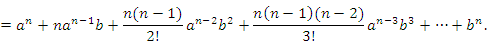
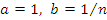 , получим , получим
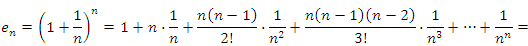
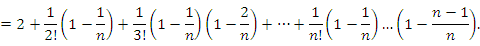
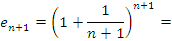
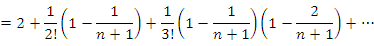
Сравним выражения для 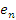 и и 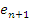 . .
Во-первых, оба эти выражения содержат только положительные слагаемые. Во-вторых, начиная со второго слагаемого, каждый член в выражении для 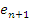 превышает соответствующий член выражения для превышает соответствующий член выражения для 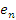 , поскольку , поскольку
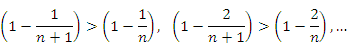
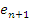 состоит из большего числа слагаемых. Следовательно, состоит из большего числа слагаемых. Следовательно, 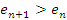
Далее докажем, что последовательность 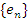 является ограниченной. Действительно, первый член любой монотонно возрастающей последовательности является ее наибольшей нижней границей и, таким образом, является ограниченной. Действительно, первый член любой монотонно возрастающей последовательности является ее наибольшей нижней границей и, таким образом, 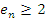 для всех натуральных значений n. для всех натуральных значений n.
Перейдем к доказательству существования верхней границы. Очевидно, что 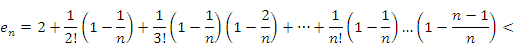
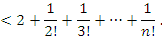
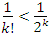 для всех k > 3. Тогда для всех k > 3. Тогда
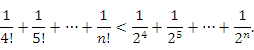
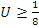 .
Таким образом, последовательность с общим членом .
Таким образом, последовательность с общим членом
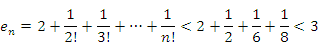
|