Теорема 4:
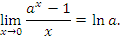
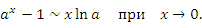
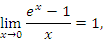
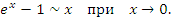
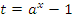 , получим , получим
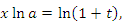
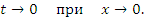
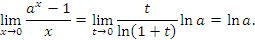
Если 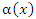 – бесконечно малая функция при x → a, то – бесконечно малая функция при x → a, то
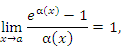
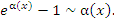
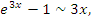
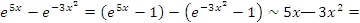
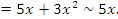
Графическая иллюстрация теоремы 4 представлена на рисунке 5. 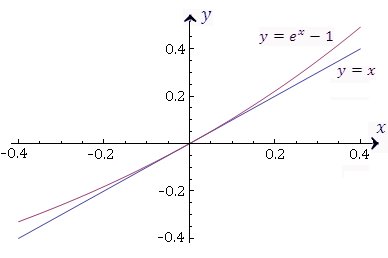
Рис 5. Прямая y = x является касательной к графику функции 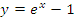 в точке x = 0. Поэтому в окрестности нуля в точке x = 0. Поэтому в окрестности нуля 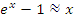 . .
|