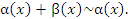Пусть 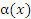 и и 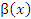 – бесконечно малые функции при – бесконечно малые функции при 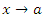 . Предел отношения этих величин может принимать любые значения – в зависимости от быстроты убывания одной величины относительно другой. Для сопоставления скоростей убывания этих величин при стремлении x точке a можно использовать предел отношения . Предел отношения этих величин может принимать любые значения – в зависимости от быстроты убывания одной величины относительно другой. Для сопоставления скоростей убывания этих величин при стремлении x точке a можно использовать предел отношения
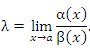 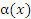 и и 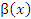 называются бесконечно малыми одного и того же порядка. называются бесконечно малыми одного и того же порядка.
Особый интерес представляет частный случай, когда λ = 1. Тогда говорят, что 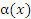 и и 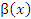 являются эквивалентными бесконечно малыми при являются эквивалентными бесконечно малыми при 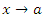 и записывают это утверждение в виде и записывают это утверждение в виде
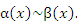
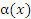 является бесконечно малой более высокого порядка по сравнению с является бесконечно малой более высокого порядка по сравнению с 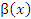 при при 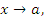 а функция а функция 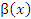 имеет меньший порядок малости. имеет меньший порядок малости.
Термин “порядок малости” допускает уточнение, если 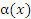 и и 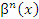 представляют собой бесконечно малые одного и того же порядка. В этом случае говорят, что представляют собой бесконечно малые одного и того же порядка. В этом случае говорят, что 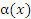 является бесконечно малой n-го порядка по сравнению с является бесконечно малой n-го порядка по сравнению с 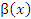 . Например, функция . Например, функция 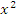 является бесконечно малой 4-го порядка по сравнению с является бесконечно малой 4-го порядка по сравнению с 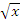 при x → 0. при x → 0.
Если λ = ∞, то бесконечно малые 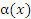 и и 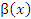 как бы меняются своими ролями. В этом случае функция как бы меняются своими ролями. В этом случае функция 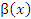 является бесконечно малой более высокого порядка по сравнению с является бесконечно малой более высокого порядка по сравнению с 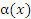 при при 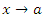 . .
Сформулируем некоторые полезные свойства эквивалентных бесконечно малых.
|
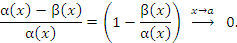
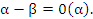
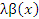 являются эквивалентными, если
являются эквивалентными, если