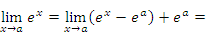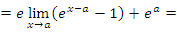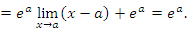|
Теорема 1. Сумма непрерывных функций есть функция непрерывная.
Доказательство. Пусть функции 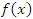 и и 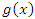 непрерывны в точке a. Тогда непрерывны в точке a. Тогда
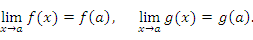
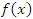 и и 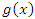 гарантирует существование предела их суммы. При этом гарантирует существование предела их суммы. При этом
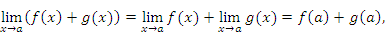
Свойство. Сумма конечного числа непрерывных функций есть функция непрерывная. Доказательство. Каждую пару непрерывных функций можно заменить одной непрерывной функцией. Затем каждую пару полученных непрерывных функций можно заменить одной непрерывной функцией. В конечном итоге останется одна непрерывная функция. Теорема 2. Произведение непрерывных функций есть функция непрерывная. Свойство. Произведение конечного числа непрерывных функций есть функция непрерывная. Теорема 3. Частное от деления непрерывных функций есть функция непрерывная – за исключением точек, в которых знаменатель обращается в нуль. Доказательство теорем 2 и 3 по своей сути не отличается от доказательства теоремы 1 и предоставляется читателю. Теорема 4. Любая элементарная функция непрерывна в области своего определения. Для доказательства этой теоремы нужно показать, что для любого числа a из области определения элементарной функции 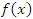 выполняется условие выполняется условие
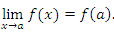
Теорема 5. Пусть функция 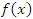 непрерывна на промежутке [a,b] и принимает на его концах значения разных знаков. Тогда на этом промежутке существует такая точка c, в которой непрерывна на промежутке [a,b] и принимает на его концах значения разных знаков. Тогда на этом промежутке существует такая точка c, в которой 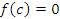 . .
Действительно, непрерывность функции на некотором промежутке означает отсутствие скачков функции на этом промежутке. Другими словами, 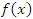 принимает все значения, заключенные между ее минимальным и максимальным значениями на промежутке [a,b], одним из которых является нулевое значение. принимает все значения, заключенные между ее минимальным и максимальным значениями на промежутке [a,b], одним из которых является нулевое значение.
Отметим, что теорема 5 лежит в основе численных методов решения уравнений. |
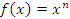 , где n – целое положительное число. Тогда
, где n – целое положительное число. Тогда
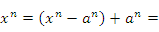
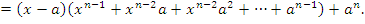
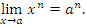
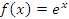 является непрерывной в каждой точке a. Действительно,
является непрерывной в каждой точке a. Действительно,