Последовательность 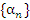 называется бесконечно малой (б/м), если значения всех ее элементов – начиная с некоторого номера – становятся по абсолютной величине меньшими любого положительного числа ε. называется бесконечно малой (б/м), если значения всех ее элементов – начиная с некоторого номера – становятся по абсолютной величине меньшими любого положительного числа ε.
Можно сказать и иначе: последовательность 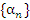 является бесконечно малой, если для любого положительного числа ε существует лишь конечное число ее членов, превосходящих ε.
В символической форме это утверждение записывается в виде является бесконечно малой, если для любого положительного числа ε существует лишь конечное число ее членов, превосходящих ε.
В символической форме это утверждение записывается в виде
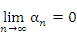
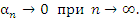
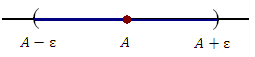
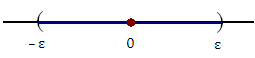
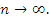 Отметим, что открытый интервал Отметим, что открытый интервал 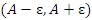 с центром в точке A называется ε-окрестностью точки A. В частности, ε-окрестность нуля представляет собой открытый интервал (-ε,ε). с центром в точке A называется ε-окрестностью точки A. В частности, ε-окрестность нуля представляет собой открытый интервал (-ε,ε).
Любая ε-окрестность нуля содержит все точки бесконечно малой последовательности 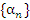 , начиная с некоторого номера. , начиная с некоторого номера.

Рис. 6. Вне ε-окрестности нуля может находиться лишь конечное число точек бесконечно малой последовательности. 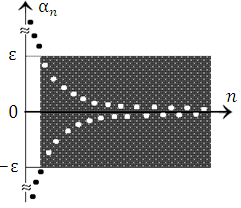
Рис. 7. Осциллирующая бесконечно малая последовательность. |