|
Понятие предела последовательности возникает на интуитивном уровне уже на самом раннем этапе изучения математики. В качестве примера обратимся к задаче о нахождении площади круга радиуса r с помощью геометрических построений.
Пусть в окружность вписан треугольник или квадрат. Понятно, что площадь такой фигуры имеет мало общего с площадью круга. Если же увеличивать и увеличивать число сторон вписанного правильного многоугольника, то его контуры постепенно станут приобретать очертания окружности. Обозначим площадь вписанного многоугольника символом 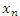 , где индекс n указывает число сторон многоугольника. Выражаясь формально, можно сказать, что , где индекс n указывает число сторон многоугольника. Выражаясь формально, можно сказать, что 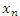 представляет собой обший член монотонно возрастающей ограниченной последовательности площадей вписанных многоугольников. При неограниченном вохрастании n элементы этой последовательности все точнее и точнее описывают площадь круга. Несколько забегая вперед, можно сказать, что последовательность представляет собой обший член монотонно возрастающей ограниченной последовательности площадей вписанных многоугольников. При неограниченном вохрастании n элементы этой последовательности все точнее и точнее описывают площадь круга. Несколько забегая вперед, можно сказать, что последовательность 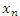 имеет своим пределом площадь круга. имеет своим пределом площадь круга.
Рассмотрим теперь последовательность 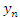 , n-ый элемент которой равен площади описанного многоугольника, имеющего n сторон. В этом случае мы имеем дело с монотонно убывающей ограниченной последовательностью площадей описанных многоугольников, которая при неограниченном вохрастании n все точнее и точнее описывает площадь круга. , n-ый элемент которой равен площади описанного многоугольника, имеющего n сторон. В этом случае мы имеем дело с монотонно убывающей ограниченной последовательностью площадей описанных многоугольников, которая при неограниченном вохрастании n все точнее и точнее описывает площадь круга.

Рис. 10. Площадь круга есть предельное значение площадей вписанных и описанных многоугольников при увеличении числа сторон. Число A называется пределом последовательности 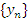 , если разность , если разность 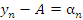 является бесконечно малой величиной.
Другими словами, число A является пределом последовательности является бесконечно малой величиной.
Другими словами, число A является пределом последовательности 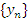 , если переменную , если переменную 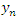 можно представить в виде можно представить в виде 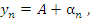 где где 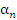 – некоторая бесконечно малая величина. Символически такое утверждение записывают в виде – некоторая бесконечно малая величина. Символически такое утверждение записывают в виде
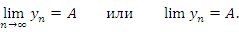
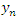 стремится к числу A: стремится к числу A:
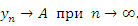
Если 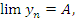 , то любая ε-окрестность точки A содержит все точки , то любая ε-окрестность точки A содержит все точки 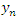 , начиная с некоторого номера. Вне этой окрестности может находиться разве что конечное число точек , начиная с некоторого номера. Вне этой окрестности может находиться разве что конечное число точек 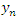 . .
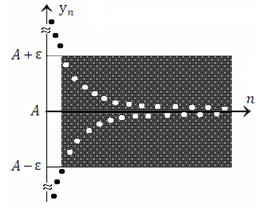
Рис. 11. Последовательность 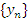 имеет своим пределом число A. имеет своим пределом число A.
Последовательность, имеющая конечный предел, называется сходящейся. В противном случае последовательность называется расходящейся. 
Рис. 12. Иллюстрация сходимости последовательности 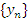 к числу A. к числу A.
Примерами расходящихся последовательностей являются последовательности с общими членами 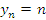 и и 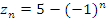 , первая из которых стремится к ∞ с ростом n, а вторая – не имеет предела при , первая из которых стремится к ∞ с ростом n, а вторая – не имеет предела при 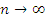 . .
|