|
Условимся, что если не оговорено противное, то под угловой мерой всегда понимается радианная мера.
Первый замечательный предел устанавливает эквивалентность между синусом бесконечно малого аргумента и самим аргументом: 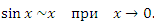 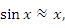 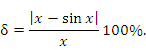 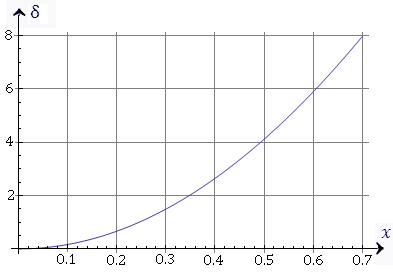
Рис. 8. Ошибка вычислений синуса по формуле 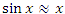 достигает 4% лишь при x ≈ 0.5 радиан, что составляет примерно 29°. достигает 4% лишь при x ≈ 0.5 радиан, что составляет примерно 29°. Для приближенных вычислений значений косинуса можно использовать равенство 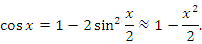 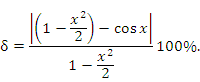
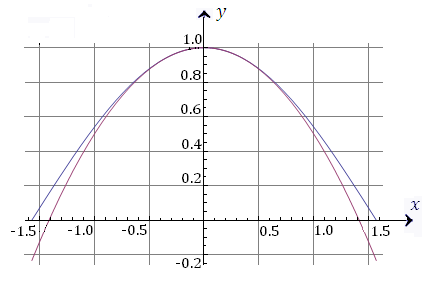
Рис. 9. Графики функции 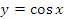 (верхняя кривая) и параболы (верхняя кривая) и параболы 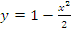 (нижняя кривая). (нижняя кривая).
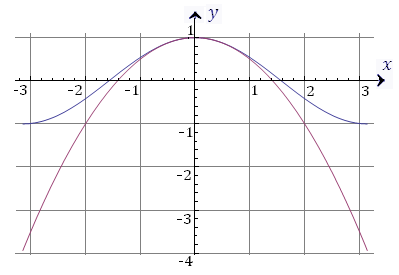
Рис. 10. Графики функций 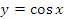 и и 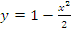 в более широком диапазоне изменений аргумента. в более широком диапазоне изменений аргумента.
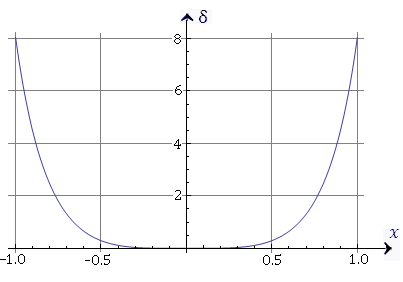
Ошибка вычислений косинуса по формуле 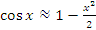 достигает 8% при достигает 8% при 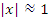 радиан, что примерно равно 57°. При радиан, что примерно равно 57°. При 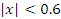 радиан относительная погрешность вычислений составляет менее 0.7%. радиан относительная погрешность вычислений составляет менее 0.7%. Формула аппроксимации тангенса значением его аргумента имеет значительно меньшую область применимости. Результаты расчетов представлены на рисунке 12. 
Рис. 12. Прямая y = x является касательной к графику функции 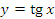 в точке x = 0. Очевидно, что в точке x = 0. Очевидно, что 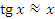 в окрестности нуля. в окрестности нуля. Относительная погрешность вычислений тангенса по формуле 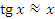 представлена на рисунке 13, где представлена на рисунке 13, где
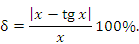
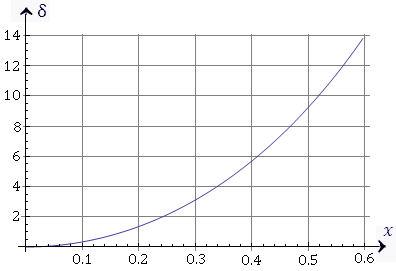 Рис. 13. Ошибка вычислений тангенса по формуле 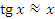 достигает 14% уже при x ≈ 0.6 радиан. достигает 14% уже при x ≈ 0.6 радиан.
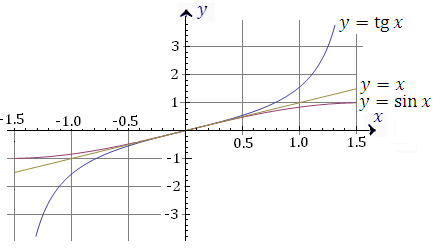
Рис. 14. Сопоставление графиков функций 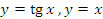 и и 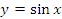 в окрестности нуля. в окрестности нуля. Формула 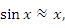 имеет более широкий диапазон применимости, чем формула имеет более широкий диапазон применимости, чем формула 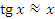 . Однако ситуация изменяется на противоположную при переходе к обратным функциям. Соответствующие иллюстрации представлены на рисунке 15. . Однако ситуация изменяется на противоположную при переходе к обратным функциям. Соответствующие иллюстрации представлены на рисунке 15.
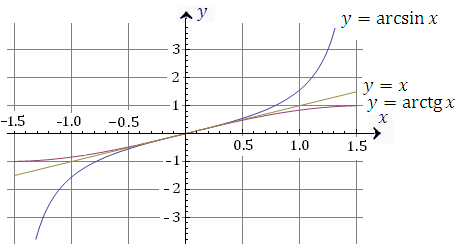
Рис. 15. Графики функций 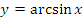 , y = x и , y = x и 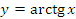 в окрестности нуля. в окрестности нуля.
|