Бесконечно малые последовательности (примеры)


-
Последовательность с общим членом
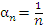 является бесконечно малой, поскольку все ее члены, начиная с некоторого номера, становятся меньше любого положительного числа ε. является бесконечно малой, поскольку все ее члены, начиная с некоторого номера, становятся меньше любого положительного числа ε.
Действительно, неравенство 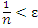 эквивалентно неравенству эквивалентно неравенству 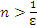 и, следовательно, выполняется для всех и, следовательно, выполняется для всех  одновременно, если в качестве номера N выбрать любое целое число, которое больше, чем одновременно, если в качестве номера N выбрать любое целое число, которое больше, чем 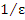 . Полагая, например, ε = 0.001, получаем, что . Полагая, например, ε = 0.001, получаем, что 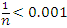 для всех n > 1000. для всех n > 1000.
Бытовая интерпретация этого результата вполне очевидна: достаточно вообразить себе пирог, который мы пытаемся разделить сначала на 1000, затем на 1000000 и так далее гостей. При этом гости продолжают прибывать, так что вопрос: "Сколько же достанется каждому?" представляется вполне риторическим.
|
***
***
|