Пусть кривая лежит в плоскости x0y и описывается уравнением r = r(φ) в полярных координатах. Представим выражение 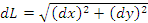 в виде в виде
Выразим декартовые координаты x и y через полярные координаты r и φ:
|
Пусть кривая лежит в плоскости x0y и описывается уравнением r = r(φ) в полярных координатах. Представим выражение 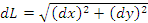 в виде в виде
Выразим декартовые координаты x и y через полярные координаты r и φ:
|