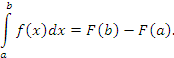|
Геометрические и физические характеристики можно представить в виде суммы бесконечно малых элементов, составляющих целое. Например, площадь плоской области можно разбить на сумму площадей бесконечно малых прямоугольников, а массу тела с переменной плотностью можно рассматривать как сумму масс элементов, в пределах каждого из которых плотность является постоянной.
Процедура суммирования такого рода элементов и называется интегрированием. В примере с площадью фигуры фактически суммируются (интегрируются) высоты прямоугольников, умноженные на их основания, а в примере с массой тела суммируются плотности ячеек, умноженные на их объемы. |
|||||||||||||||||
Пусть функция f(x) определена на интервале [a,b]. Разобьем этот интервал на n элементов 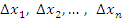 . .
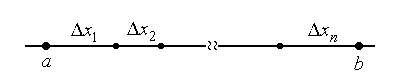
Рис. 1. Разбиение интервала [a,b] на элементы. Внутри каждого промежутка 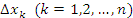 выберем произвольным образом точку выберем произвольным образом точку 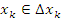 , вычислим значения функции f(x) в этих точках и составим произведения и составим произведения , вычислим значения функции f(x) в этих точках и составим произведения и составим произведения 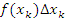 . Сумма полученных произведений называется интегральной суммой: . Сумма полученных произведений называется интегральной суммой:
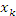 могут быть, в частности, выбраны в серединах интервалов могут быть, в частности, выбраны в серединах интервалов 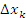 или в их концевых точках. Если функция f(x) является положительно определенной, то произведение вида или в их концевых точках. Если функция f(x) является положительно определенной, то произведение вида 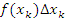 можно интерпретировать как площадь прямоугольника с основанием можно интерпретировать как площадь прямоугольника с основанием 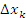 и высотой и высотой 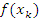 . .
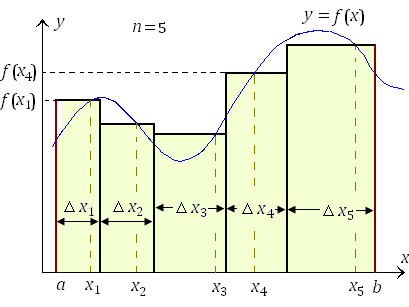
Рис. 2. Геометрическая интерпретация интегральной суммы при n = 5. С увеличением числа элементов разбиения интервала [a,b] интегральная сумма 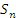 все более точно аппроксимирует площадь фигуры, ограниченной сверху кривой все более точно аппроксимирует площадь фигуры, ограниченной сверху кривой 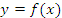 , снизу – осью 0x, а с боков – вертикальными отрезками x = a и x = b (то есть площадь криволинейной трапеции, показанной на рисунке 3). , снизу – осью 0x, а с боков – вертикальными отрезками x = a и x = b (то есть площадь криволинейной трапеции, показанной на рисунке 3).
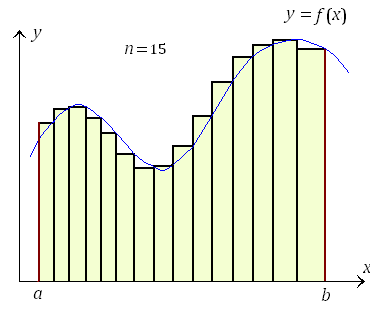
Рис. 3. При разбиении промежутка [a,b] на большее число меньших частей увеличивается число прямоугольников, сумма площадей которых более точно аппроксимирует площадь криволинейной трапеции. Далее выполним предельный переход 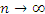 , обеспечивая при этом, чтобы все , обеспечивая при этом, чтобы все 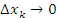 . Если существует предел интегральной суммы (1), который не зависит от способа разбиения интервала [a,b] и выбора точек . Если существует предел интегральной суммы (1), который не зависит от способа разбиения интервала [a,b] и выбора точек 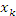 , то этот предел называется определенным интегралом от функции f(x) по промежутку [a,b] и обозначается символическим выражением , то этот предел называется определенным интегралом от функции f(x) по промежутку [a,b] и обозначается символическим выражением
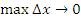 , то все , то все 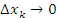 и и 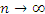 . При стремлении . При стремлении 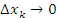 к нулю каждое слагаемое суммы (2) стремится к нулю, но при этом число слагаемых стремится к бесконечности. Результатом этих двух взаимно противоположных стремлений является некое число, называемое определенным интегралом. к нулю каждое слагаемое суммы (2) стремится к нулю, но при этом число слагаемых стремится к бесконечности. Результатом этих двух взаимно противоположных стремлений является некое число, называемое определенным интегралом.
Величины a и b называются соответственно нижним и верхним пределами интегрирования, а процедура вычисления интеграла (2) называется интегрированием. Обозначение интеграла в виде 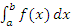 введено Лейбницем, где f(x)dx напоминает о слагаемое суммы введено Лейбницем, где f(x)dx напоминает о слагаемое суммы 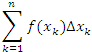 , а символ ∫ представляет собой стилизованную начальную букву латинского слова "Summa". , а символ ∫ представляет собой стилизованную начальную букву латинского слова "Summa".
Если 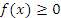 на промежутке [a,b], то интегральная сумма на промежутке [a,b], то интегральная сумма 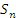 стремится к площади криволинейной трапеции и, таким образом, интеграл стремится к площади криволинейной трапеции и, таким образом, интеграл 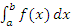 равен площади области, ограниченной графиком функции y = f(x) и осью 0x от x = a до x = b. равен площади области, ограниченной графиком функции y = f(x) и осью 0x от x = a до x = b.
Пусть F(x) - первообразная функции f(x) : 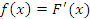
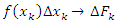 при при 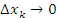 , где , где 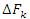 - изменение функции F(x) на промежутке - изменение функции F(x) на промежутке 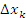 . Следовательно, . Следовательно,
|
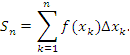
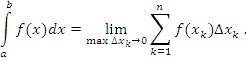
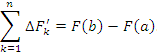 ,
,