Формула интегрирования по частям для определенных интегралов вытекает из соответствующей формулы для неопределенных интегралов и имеет вид
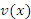 – любые дифференцируемые функции. – любые дифференцируемые функции.
Формула (1) позволяет свести одну проблему интегрирования к другой. Так, если можно вычислить один из интегралов, Во-первых, подынтегральную функцию f(x) нужно представить в виде произведения некоторых функций u(x) и 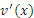 : :
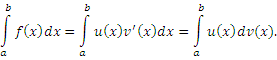
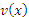 , нужно продифференцировать u(x) и проинтегрировать , нужно продифференцировать u(x) и проинтегрировать 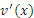 : :
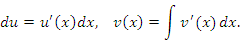
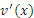 , поскольку не существует универсального правила, применимого во всех случаях. Понимание приходит только с опытом. Поэтому на первых порах сделайте какой-нибудь выбор и посмотрите – будет ли полученный интеграл проще исходного. Если нет, то сделайте другой выбор, перебирая различные варианты до тех пор, пока не будет найден наилучший. Обычно достаточно решить несколько примеров, чтобы научиться сразу делать правильный выбор. В качестве ориентиров можно использовать следующие простые критерии. , поскольку не существует универсального правила, применимого во всех случаях. Понимание приходит только с опытом. Поэтому на первых порах сделайте какой-нибудь выбор и посмотрите – будет ли полученный интеграл проще исходного. Если нет, то сделайте другой выбор, перебирая различные варианты до тех пор, пока не будет найден наилучший. Обычно достаточно решить несколько примеров, чтобы научиться сразу делать правильный выбор. В качестве ориентиров можно использовать следующие простые критерии.
(A): Интеграл от 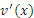 должен вычисляться достаточно просто. должен вычисляться достаточно просто.
(B): Производная от u(x) должна быть достаточно простой функцией (желательно, более простой, чем сама функция u(x)). |
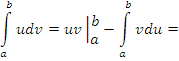
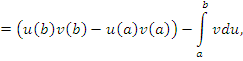
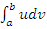 или
или 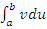 , то можно вычислить и другой, выразив его через известный. В этом и заключается суть метода интегрирования по частям.
, то можно вычислить и другой, выразив его через известный. В этом и заключается суть метода интегрирования по частям.