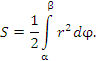|
Характеристики геометрических фигур (площади, длины и так далее) можно представить в виде суммы составных элементов. Например, площадь фигуры можно рассматривать как суумму площадей бесконечно малых прямоугольников, секторов или иных частей, составляющих целое. Процедура суммирования такого рода элементов и представляет собой интегрирование.
Все, что для этого требуется, это формула для соответствующей характеристики, относящаяся к бесконечно малому элементу. Для вычисления площади S некоторой области нужно получить формулу для dS. Длина дуги кривой l представляет собой сумму длин dl ее элементов. Объем фигуры V равен сумме объемов dV "ломтиков" с бесконечно малыми толщинами. И так далее. |
|
|
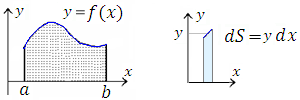
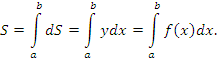


 ,
,
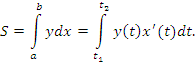
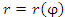 , заданной в полярной системе координат, и лучами
, заданной в полярной системе координат, и лучами 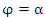 и
и 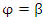 .
.
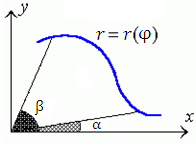
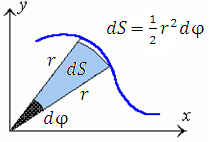
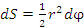 и
и