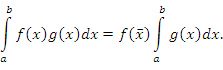|
Различные геометрические и физические величины можно представить в виде суммы бесконечно малых элементов, составляющих целое. Например, площадь плоской области можно разбить на сумму площадей бесконечно малых прямоугольников, а массу тела с переменной плотностью можно рассматривать как сумму масс элементов, в пределах каждого из которых плотность является постоянной.
Процедура суммирования такого рода элементов и называется интегрированием. В примере с площадью фигуры фактически суммируются (интегрируются) высоты прямоугольников с одинаковыми основаниями, а в примере с массой тела суммируются плотности ячеек одинакового объема. |
|
|
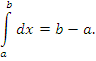
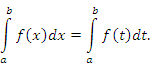
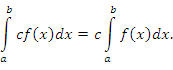
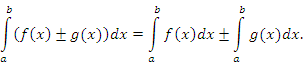
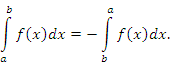
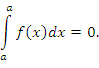
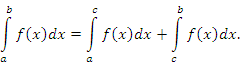
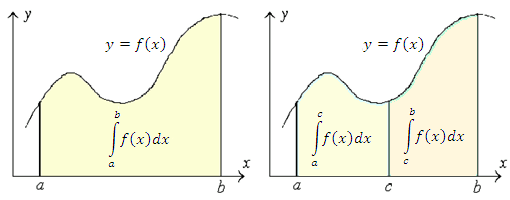
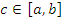 (см. рисунок 1).
(см. рисунок 1).
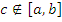 – при условии, что существуют интегралы
– при условии, что существуют интегралы 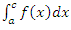 и
и 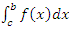 :
:
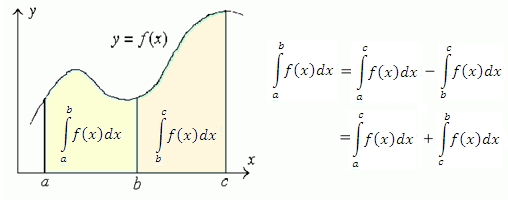
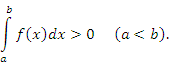
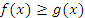 во всех точках этого промежутка. Тогда
во всех точках этого промежутка. Тогда
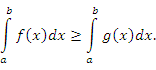
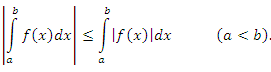
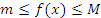 во всех точках этого промежутка. Тогда
во всех точках этого промежутка. Тогда
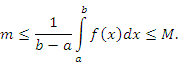
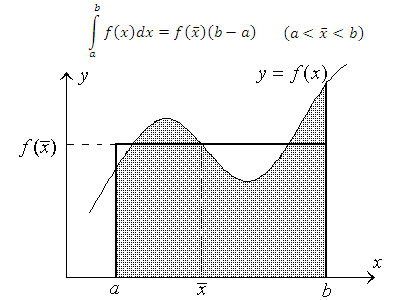
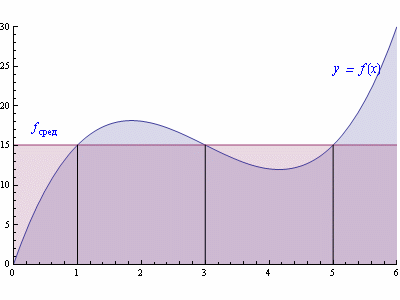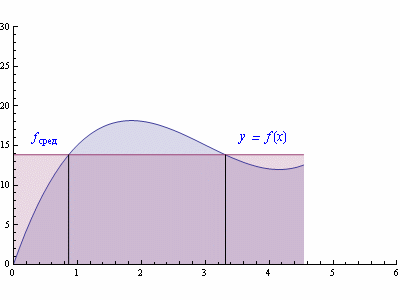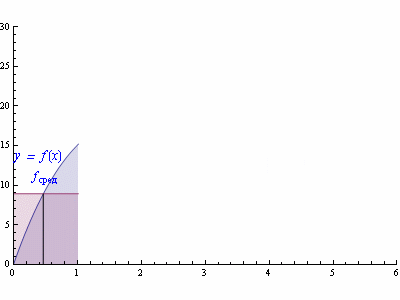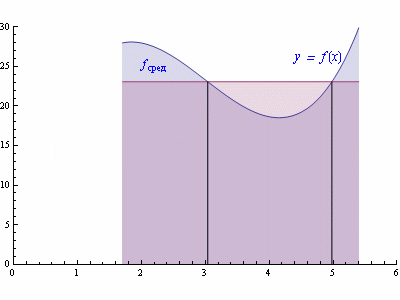
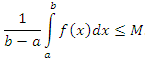 называется средним значением функции f(x) на промежутке [a,b]. Поэтому свойство 8 называют теоремой о среднем.
называется средним значением функции f(x) на промежутке [a,b]. Поэтому свойство 8 называют теоремой о среднем.
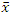 , что
, что
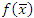 .
.