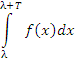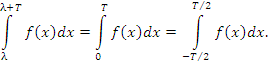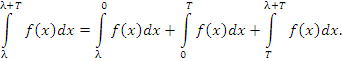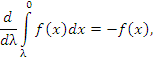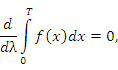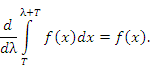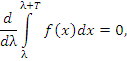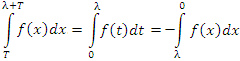Интегрирование периодических функций

Определенные интегралы

Площадь плоской фигуры Движение частицы с переменной скоростью Понятие определенного интеграла Классы интегрируемых функций Свойства интегралов Формула Ньютона–Лейбница Интегрирование заменой переменной Интегрирование по частям Интегрирование четных и нечетных функций Интегрирование периодических функций Ортогональные функции

Геометрические приложения

Площадь плоской области Длины дуги кривой, заданной в явном виде Длины дуги кривой, заданной в параметрическом виде Длины дуги кривой, заданной в полярных координатах Объемы тел

Теореиа. Пусть f(x) – интегрируемая на промежутке [0,T] периодическая функция с периодом T:

f(x + T) = f(x).

(1)

Тогда интеграл

(2)

не зависит от λ. В частности,

(3)

Доказательство 1. Представим рассматриваемый интеграл в виде суммы трех интегралов:

(4)

Вычислим производную по λ от выражения в правой части этого равенства:

(5)

Таким образом,

(6)

что и требовалось доказать.

Доказательство 2. Представим рассматриваемый интеграл в виде суммы (4) и преобразуем последний интеграл в правой части, выполнив замену переменной x = t + T. Очевидно, что этот интеграл лишь знаком отличается от первого интеграла в правой части равенства (4):

(7)

Конев В.В. Определенные интегралы