Теорема. Пусть функция f(x) является непрерывной на промежутке [a,b] относительно переменной x, которая в свою очередь является функцией 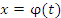 переменной t на промежутке переменной t на промежутке 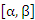 и имеет на нем непрерывную производную. Если и имеет на нем непрерывную производную. Если 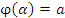 и и 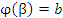 , то , то
|
Теорема. Пусть функция f(x) является непрерывной на промежутке [a,b] относительно переменной x, которая в свою очередь является функцией 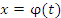 переменной t на промежутке переменной t на промежутке 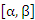 и имеет на нем непрерывную производную. Если и имеет на нем непрерывную производную. Если 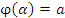 и и 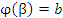 , то , то
|