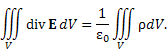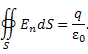Конев В.В.  Скалярные и векторные поля

| Словарь | Калькулятор | Тесты | Задачи и упражнения |
| Скалярные и векторные поля. Градиент | Ротор. Типы полей. Системы координат |
Соленоидальное поле при наличии особых точек
      В силу теоремы Остроградского-Гаусса поток соленоидального поля  A  через любую замкнутую поверхность равен нулю. Однако при наличии особых точек, в которых вектор поля не определен и дивергенция отлична от нуля, поток через замкнутую поверхность, окружающую одну или несколько особых точек, может быть отличен от нуля, но принимает одно и тоже значение для всех таких замкнутых поверхностей.
     Это объясняется тем обстоятельством, что ненулевой вклад в тройной интеграл от  div A  вносят только бесконечно малые окрестности особых точек и, следовательно, форма поверхности не имеет никакого значения (см рисунок 1).

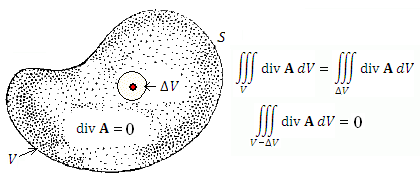Рис. 1. Поток векторного поля  A  через поверхность  S  равен потоку вектора  A  через границу бесконечно малой окрестности особой точки.
     Если же источники поля расположены за пределами замкнутой поверхности, то поток поля через эту поверхность равен нулю. Действительно, пусть источником поля является точка  q.

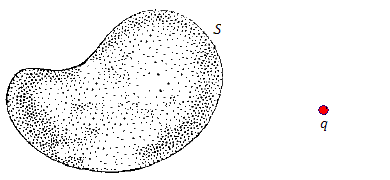Рис. 2. Особая точка соленоидального поля расположена за пределами области, ограниченной поверхностью  S.
     Окружим точку  q  замкнутой поверхностью  S1  и обозначим поток поля  A  через эту поверхность символом  Ф.

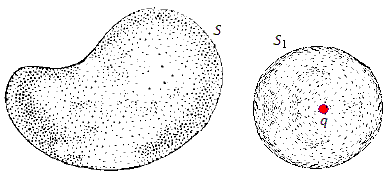Рис. 3. Источником векторного поля является особая точка  q . Поток поля через окружающую эту точку поверхность не зависит от формы поверхности.
     Затем соединим области, ограниченные поверхностями  S  и  S1 , трубкой бесконечно малого поперечного сечения.

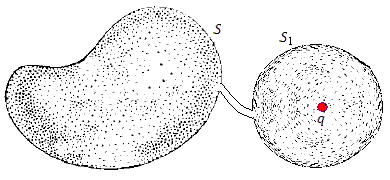Рис. 4. Величина потока через замкнутую поверхность не изменяется при деформации поверхности.
      Поскольку поток поля через поверхность тонкой трубки равен нулю, то равен нулю и поток через поверхность  S.
     Этим свойствам можно дать наглядную физическую интерпретацию. Проинтенрируем обе части уравнения Максвелла
по объему V, ограниченному некоторой поверхностью S:
Интеграл от плотности ρ распределения заряда равен заряду q, находящемуся в объеме V, тогда как интеграл от дивергенции равен потоку векторного поля через поверхность S.
     Физики называют это уравнение теоремой Гаусса, которая выражает собой тот факт, что поток электрического поля  E  через замкнутую поверхность не зависит от размеров и формы этой поверхности, а определяется только величиной заряда, находящегося в объеме V. Поток поля внешних зарядов, расположенных за пределами поверхности, равен нулю.