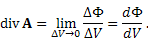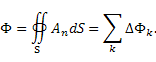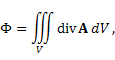Физические величины обладают одинаковыми свойствами, если их определения математически эквивалентны. Сопоставим между собой определения плотности распределения массы вещества и дивергенция векторного поля.
-
Плотность ρ распределения массы определяется как предел отношения массы, заключенной в объеме ΔV, к величине этого объема при стремлении ΔV к нулю (то есть при стягивании области ΔV в точку):
 .
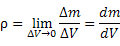Масса тела обладает свойством аддитивности, согласно которому сумма масс всех элементов, образующих тело, равна массе всего тела:
 .
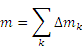Масса вещества, заключенного в некоторой области, равна интегралу от плотности по этой области:
 .
-
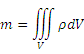Дивергенция векторного поля A определяется как предел отношения потока поля через поверхность, ограничивающую область объема ΔV, к величине этого объема при стремлении ΔV к нулю (при стягивании области ΔV в точку):
Поток векторного поля через поверхность замкнутой области обладает свойством аддитивности, согласно которому сумма потоков поля из всех элементов, образующих эту область, равна потоку поля через поверхность, ограничивающую область:
Есть ли у нас альтернатива заключению
которое выражает тот факт, что интеграл от производной функции равен этой функции?
Именно это утверждение составляет суть теоремы Остроградского-Гаусса.
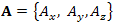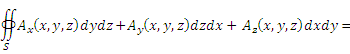
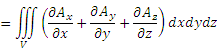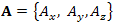Теорема Остроградского-Гаусса в координатной форме.  Поток векторного поля  через замкнутую кусочно-гладкую поверхность S в направлении внешней нормали равен тройному интегралу от div A по области V, ограниченной поверхностью S :
 .
|
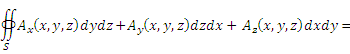
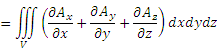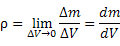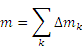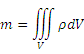