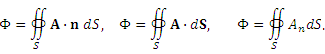Потоком векторного поля
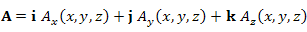 ,
через поверхность S называется поверхностный интеграл второго рода от векторной функции A (x, y, z) по поверхности S,
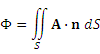 ,
где n – единичный вектор внешней нормали к поверхности S.
 Используются и другие формы записи выражения для потока поля. Например, с учетом того, что скалярное произведение A · n представляет собой проекцию An вектора A на направление внешней нормали n к поверхности S.
Используются и другие формы записи выражения для потока поля. Например, с учетом того, что скалярное произведение A · n представляет собой проекцию An вектора A на направление внешней нормали n к поверхности S.
 Еще один способ обозначения связан с введением вектора dS = n dS, величина которого равна площади элемента поверхности dS, а направление определяется вектором n.
Еще один способ обозначения связан с введением вектора dS = n dS, величина которого равна площади элемента поверхности dS, а направление определяется вектором n.
 Таким образом,
Таким образом,
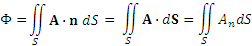 .
Рисунок 1 иллюстрирует понятие потока векторного поля A через малый элемент поверхности. Поток поля принимает наибольшее значение, если вектор A направлен перепендикулярно к поверхности.
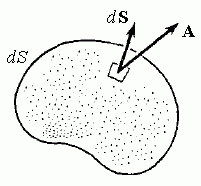 .
Рис. 1. Поток векторного поля A через бесконечно малый элемент поверхности d S равен скалярному произведению 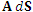 .
 В координатной форме поток векторного поля записывается в вмде
В координатной форме поток векторного поля записывается в вмде
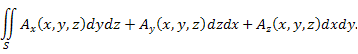 .
Вычисление потока векторного поля сводится к вычислению суммы трех двойных интегралов
где плоские области 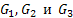 представляют собой проекции поверхности S на координатные плоскости представляют собой проекции поверхности S на координатные плоскости 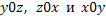 соответственно. Выражения соответственно. Выражения 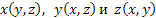 получаются из уравнения получаются из уравнения 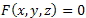 поверхности S, разрешением относительно соответствующих координат. поверхности S, разрешением относительно соответствующих координат.
 Для обозначения потока векторного поля через замкнутую поверхность используются выражения вида
Для обозначения потока векторного поля через замкнутую поверхность используются выражения вида
|
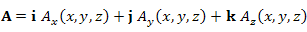 ,
,
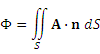 ,
,
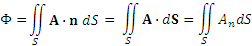 .
.
 .
.
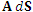 .
.
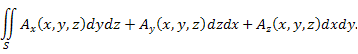 .
.
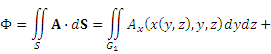
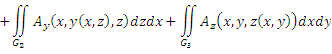
 представляют собой проекции поверхности S на координатные плоскости
представляют собой проекции поверхности S на координатные плоскости 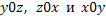 соответственно. Выражения
соответственно. Выражения 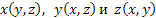 получаются из уравнения
получаются из уравнения 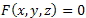 поверхности S, разрешением относительно соответствующих координат.
поверхности S, разрешением относительно соответствующих координат.