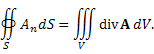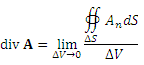Теорема. Поток векторного поля A через замкнутую кусочно-гладкую поверхность S в направлении внешней нормали равен тройному интегралу от div A по области V, ограниченной поверхностью S :
Доказательство. Разобъем область V на малые элементы ΔV (как это показано на рисунке 1). Разобъем область V на малые элементы ΔV (как это показано на рисунке 1).
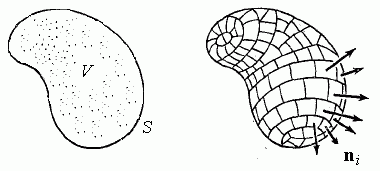 Рис. 1
Рис. 1. Разбиение области V, ограниченной поверхностью
S, на малые элементы Δ Vk , границами которых являются поверхности Δ Sk .
 Согласно определению дивергенции векторного поля,
Согласно определению дивергенции векторного поля,
Определение дивергенции вектора
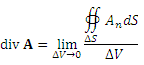
Здесь ΔΦ – поток вектора A из области, ограниченной поверхностью ΔS, ΔV – объем этой области.
|
поток ΔΦk поля A через поверхность ΔSk малой области ΔVk можно представить в виде приближенного равенства
 Далее выполним суммирование по всем элементам области V и осуществим предельный переход, переходя к бесконечно малым элементам.
Далее выполним суммирование по всем элементам области V и осуществим предельный переход, переходя к бесконечно малым элементам.
 Согласно свойствам потока векторного поля, сумма потоков из всех частей объема V равна потоку вектора A через внешнюю поверхность S:
Согласно свойствам потока векторного поля, сумма потоков из всех частей объема V равна потоку вектора A через внешнюю поверхность S:
 Сумма произведений
Сумма произведений 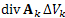 по всем элементам разбиения области V представляет собой интегральную сумму от div A по этой области и, следовательно, по всем элементам разбиения области V представляет собой интегральную сумму от div A по этой области и, следовательно,
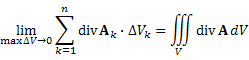 .
Таким образом,
|
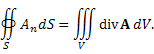

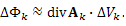
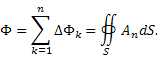
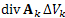 по всем элементам разбиения области V представляет собой интегральную сумму от div A по этой области и, следовательно,
по всем элементам разбиения области V представляет собой интегральную сумму от div A по этой области и, следовательно,
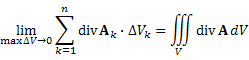 .
.